题目内容
10．在正三角形、正方形、正五边形、正六边形中不能单独镶嵌平面的是（ ）| A． | 正三角形 | B． | 正方形 | C． | 正五边形 | D． | 正六边形 |
分析 分别求出各个正多边形的每个内角的度数，再利用镶嵌应符合一个内角度数能整除360即可作出判断．
解答 解：A．正三角形的每个内角是60°，能整除360°，能密铺；
B．正方形的每个内角是90°，4个能密铺；
C．正五边形每个内角是180°-360°÷5=108°，不能整除360°，不能密铺；
D．正六边形的每个内角是120°，3个能密铺，
故选C．
点评 本题考查正多边形的镶嵌，看是否符合一个内角度数能整除360°是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E，使DE=5，折痕为PQ，则PQ的长为13．
18．如图，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
5．
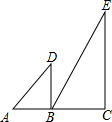如图，在直线AC的同侧有Rt△ABD和Rt△BCE，已知∠ABD=∠C=90°，∠A=45°，∠E=30°，若将△ABD绕点B按顺时针方向旋转，当AD∥BC时，旋转的角度是（ ）
如图，在直线AC的同侧有Rt△ABD和Rt△BCE，已知∠ABD=∠C=90°，∠A=45°，∠E=30°，若将△ABD绕点B按顺时针方向旋转，当AD∥BC时，旋转的角度是（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
15．若分式方程$\frac{x}{x-1}$-$\frac{m}{1-x}$=2无解，则m的值是（ ）
| A． | 1 | B． | -1 | C． | 1或-1 | D． | 0 |
2．代数式$\sqrt{1-x}$有意义，则x的取值范围是（ ）
| A． | x＞1，且x≠0 | B． | x≥1 | C． | x≠1 | D． | x≤1 |
20．单项式-$\frac{{2}^{2}x{y}^{2}}{5}$ 的次数是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |