题目内容
1. 如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E,使DE=5,折痕为PQ,则PQ的长为13.
如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E,使DE=5,折痕为PQ,则PQ的长为13.
分析 先过点P作PM⊥BC于点M,利用三角形全等的判定得到△PQM≌△ADE,从而求出PQ=AE.
解答  解:过点P作PM⊥BC于点M,
解:过点P作PM⊥BC于点M,
由折叠得到PQ⊥AE,
∴∠DAE+∠APQ=90°,
又∠DAE+∠AED=90°,
∴∠AED=∠APQ,
∵AD∥BC,
∴∠APQ=∠PQM,
则∠PQM=∠APQ=∠AED,∠D=∠PMQ,PM=AD
∴△PQM≌△ADE
∴PQ=AE=$\sqrt{{5}^{2}+1{2}^{2}}$=13.
故答案是:13.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在正三角形、正方形、正五边形、正六边形中不能单独镶嵌平面的是( )
| A. | 正三角形 | B. | 正方形 | C. | 正五边形 | D. | 正六边形 |
11.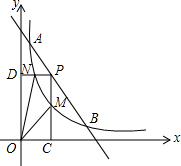 如图,一次函数与反比例函数的图象交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N,则四边形PMON面积的最大值是( )
如图,一次函数与反比例函数的图象交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N,则四边形PMON面积的最大值是( )
 如图,一次函数与反比例函数的图象交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N,则四边形PMON面积的最大值是( )
如图,一次函数与反比例函数的图象交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N,则四边形PMON面积的最大值是( )| A. | $\frac{25}{2}$ | B. | $\frac{25}{3}$ | C. | 6 | D. | 12 |
 如图,已知抛物线经过原点o和x轴上一点A(4,0),抛物线顶点为E,它的对称轴与x轴交于点D.直线y=-2x-1经过抛物线上一点B(-2,m)且与y轴交于点C,与抛物线的对称轴交于点F.
如图,已知抛物线经过原点o和x轴上一点A(4,0),抛物线顶点为E,它的对称轴与x轴交于点D.直线y=-2x-1经过抛物线上一点B(-2,m)且与y轴交于点C,与抛物线的对称轴交于点F. 如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为6,则k=6.
如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为6,则k=6. 若以A(1,2),B(-1,0),C(2,0)三点为顶点要画平行四边形,则第四个顶点坐标为(-1,2)或(4,2)或(0,-2).
若以A(1,2),B(-1,0),C(2,0)三点为顶点要画平行四边形,则第四个顶点坐标为(-1,2)或(4,2)或(0,-2). 如图,△ABC≌△ADE,BC的延长线交DE于点G,若∠B=24°,∠CAB=54°,∠DAC=16°,则∠DGB=70°.
如图,△ABC≌△ADE,BC的延长线交DE于点G,若∠B=24°,∠CAB=54°,∠DAC=16°,则∠DGB=70°.