题目内容
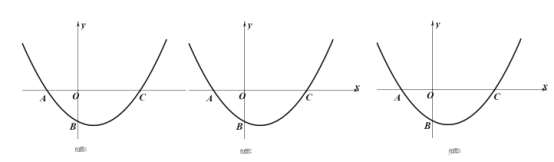
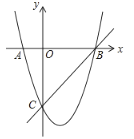
【题目】如图，在平面直角坐标系中，点
为坐标原点．抛物线
交
轴于
、
两点，交
轴于点
，直线
经过、两点．
（1）求抛物线的解析式；
（2）过点作直线
轴交抛物线于另一点
，过点作
轴于点
，连接
，求
的值．
【答案】（1）
；（2）
【解析】
（1）首先求出点B、C的坐标，然后利用待定系数法求出抛物线的解析式；
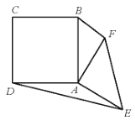
（2）如图，过点C作直线CD⊥y轴交抛物线于点D，过点D作DE⊥x轴于点E，连接BD，构造Rt△DEB，欲求锐角三角函数定义tan∠BDE＝
，先求线段BE，DE的长度即可．
（1）解：∵直线
经过
、
两点，易得点
，
，
代入抛物线
中，得
解之得
∴抛物线的解析式为．
（2）解：如图，过点作直线
轴交抛物线于点
，过点作
轴于点
，连接
．
∵抛物线的对称轴为
，点为
，
∴点为
，从而得
，
．
∵点为
∴
，
在
中，
，
∴
．
练习册系列答案
相关题目
