Question

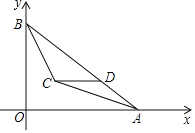
【题目】已知：如图，AB为⊙O的弦，过点O作AB的平行线，交⊙O于点C，直线OC上一点D满足∠D＝∠ACB．

（1）判断直线BD与⊙O的位置关系，并证明你的结论；

（2）若⊙O的半径等于4，tan∠ACB＝，求CD的长．

Answer 1

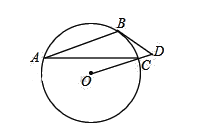
【答案】（1）详见解析；（2）CD=1

【解析】

（1）相切，连接OB，通过平行线、弦切角定理、等边对等角，得出相等的角，然后将这些相等的角进行置换，最终转换到一个三角形中，根据三角形的内角和来求出度数，从而得出∠OBD=90°．

（2）先求得∠D的正切值，在直角三角形OBD中，有半径的长和∠D的正切值，可用正弦函数求出OD的长，从而求出CD的长．

（1）直线BD与⊙O相切．

证明：如图，连接OB．

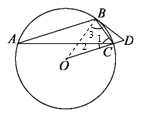
∵∠OCB=∠CBD+∠D，∠1=∠D，

∴∠2=∠CBD，

∵AB∥OC，

∴∠2=∠A，

∴∠A=∠CBD．

∵OB=OC，

∴∠BOC+2∠3=180°．

∵∠BOC=2∠A，

∴∠A+∠3=90°．

∴∠CBD+∠3=90°．

∴∠OBD=90°．

∴直线BD与⊙O相切．

（2）∵∠D=∠ACB，tan∠ACB=，
∴tan∠D=．
∵∠OBD=90°，OB=4，tan∠D=，

∴，

∴CD=OD-OC=1．