题目内容
【题目】在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴正半轴交于点
轴正半轴交于点![]() ,
,![]() .
.
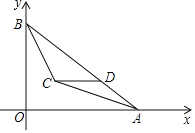
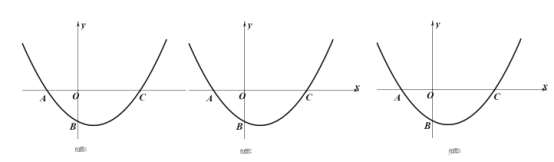
(1)如图1,求![]() 的值;
的值;
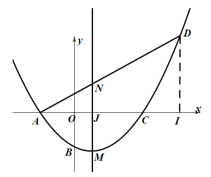
(2)如图2,抛物线的顶点坐标是![]() ,点
,点![]() 是第一象限抛物线上的一点,连接
是第一象限抛物线上的一点,连接![]() 交抛物线的对称轴于点
交抛物线的对称轴于点![]() ,设点
,设点![]() 的横坐标是
的横坐标是![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
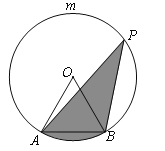
(3)如图3,在(2)的条件下,当![]() 时,过点
时,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,点
,点![]() 是
是![]() 轴下方抛物线上的一个动点,连接
轴下方抛物线上的一个动点,连接![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据![]() 得出B,C的坐标,令
得出B,C的坐标,令![]() 即可求出m的值,将B的坐标代入抛物线的解析式中即可求出a的值;
即可求出m的值,将B的坐标代入抛物线的解析式中即可求出a的值;
(2)过点D作![]() 于点I,设MN与x轴的交点为J,先利用抛物线的解析式求出M的坐标,然后利用平行线分线段成比例有
于点I,设MN与x轴的交点为J,先利用抛物线的解析式求出M的坐标,然后利用平行线分线段成比例有![]() ,代入相应的值计算即可得出答案;
,代入相应的值计算即可得出答案;
(3)先根据![]() 求出此时D,E的坐标,然后将点D的坐标代入
求出此时D,E的坐标,然后将点D的坐标代入![]() 中求出直线的解析式,设G点的坐标为
中求出直线的解析式,设G点的坐标为![]() ,利用待定系数法求出直线GE的解析式,进而求出F的坐标及
,利用待定系数法求出直线GE的解析式,进而求出F的坐标及![]() ,然后利用待定系数法求出GC,EH的解析式,进而求出H点的坐标,然后表示出
,然后利用待定系数法求出GC,EH的解析式,进而求出H点的坐标,然后表示出![]() ,然后利用
,然后利用![]() 求出m的值,进而求出直线GE的解析式,通过直线GE的解析式与抛物线解析式联立即可求出P点的坐标.
求出m的值,进而求出直线GE的解析式,通过直线GE的解析式与抛物线解析式联立即可求出P点的坐标.
(1)![]()
![]() .
.
令![]() ,
,
解得![]() ,
,
![]() ,
,
![]() ,
,
∴抛物线的解析式为![]() ,
,
将点![]() 代入得,
代入得,![]() ,
,
解得![]() ;
;
(2)如图,过点D作![]() 于点I,设MN与x轴的交点为J,
于点I,设MN与x轴的交点为J,
∵![]() ,
,
![]() ,
,
![]() .
.
∵点![]() 的横坐标是
的横坐标是![]() ,
,
∴![]() ,
,
![]() .
.
![]() 轴,
轴,![]() 轴,
轴,
![]() ,
,
![]() .
.
![]() ,
,
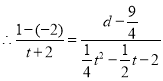 ,
,
解得![]() ;
;
(3)如图,
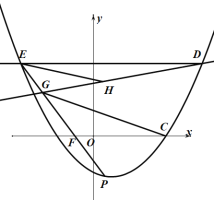
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
此时D的坐标为![]() .
.
![]() 轴,
轴,
∴点E的纵坐标也是4,
令![]() ,
,
解得![]() 或
或![]() ,
,
∴![]() .
.
∵直线![]() 经过点
经过点![]() ,
,
∴![]() ,
,
解得 ![]() ,
,
∴![]() .
.
设点G的坐标为![]() ,
,
设直线EG的解析式为![]() ,
,
将![]() 代入解析式中得
代入解析式中得
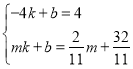 解得
解得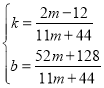
∴直线EG解析式为![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,
,
∴![]() ,
,
![]() .
.
设直线GC的解析式为![]() ,
,
将![]() 代入解析式中得
代入解析式中得
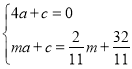 解得
解得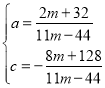
∴直线GC解析式为![]() .
.
∵![]() ,
,
∴设直线EH解析式为![]() ,
,
将点![]() 代入得
代入得![]() ,
,
解得![]() ,
,
∴直线EH解析式为![]() .
.
将直线GD的解析式与直线EH的解析式联立,
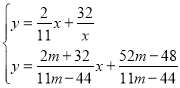 解得
解得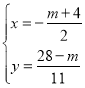
∴![]() ,
,
![]() .
.
∵![]() ,
,
∴![]()
![]() ,
,
解得![]() 或
或![]() .
.
当![]() 时,GE的解析式为
时,GE的解析式为![]() ,
,
将直线GE的解析式与抛物线的解析式联立,
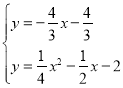 解得
解得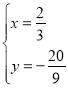 或
或![]() (点E的坐标,舍去),
(点E的坐标,舍去),
∴![]() ;
;
当![]() 时,GE的解析式为
时,GE的解析式为![]() ,
,
将直线GE的解析式与抛物线的解析式联立
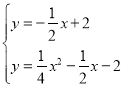 解得
解得![]() (点C的坐标,舍去) 或
(点C的坐标,舍去) 或![]() (点E的坐标,舍去),
(点E的坐标,舍去),
∴综上所述,点P的坐标为![]() .
.