题目内容
 如图,已知AB是⊙O的直径,P是AB延长线上一点,PC与⊙O相切于点C,CD⊥AB于点D,过B点作AP的垂线交PC于点F.
如图,已知AB是⊙O的直径,P是AB延长线上一点,PC与⊙O相切于点C,CD⊥AB于点D,过B点作AP的垂线交PC于点F.(1)求证:E是CD的中点;
(2)若FB=FE=2,求⊙O的半径.
考点:切线的性质
专题:
分析:(1)延长BF、AC交于点M,则结合切线可得BF=FM,再结合平行线分线段成比例可求得CE=DE;
(2)结合条件可证得PF=AF,在Rt△PFB中,可得到PF和PB的关系,再结合PC是切线利用切割线定理可得到PB和PF的关系,可求得PB的长,则可求得AO的长,即⊙O的半径.
(2)结合条件可证得PF=AF,在Rt△PFB中,可得到PF和PB的关系,再结合PC是切线利用切割线定理可得到PB和PF的关系,可求得PB的长,则可求得AO的长,即⊙O的半径.
解答: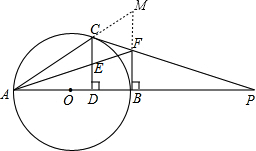 (1)证明:
(1)证明:
如图,延长BF、AC交于点M,
∵BF⊥AB,∴FB是⊙O的切线,
又CF是⊙O的切线,
∴CF=BF,
∴∠FCB=∠FBC,
又AB为直径,
∴∠BCM=90°,
∴∠B+∠M=∠BCF+∠FCM=90°,
∴∠FCM=∠M,
∴CF=MF,
∴BF=MF,
∵CD∥MB,
∴
=
=
,
∴CE=ED,
即E是CD的中点;
(2)解:
∵BF=EF=2=FC=FM,
∴∠FCE=∠FEC=∠AED,
又CD⊥AB,
∴∠FAB+∠AED=∠ECF+∠P,
∴∠FAB=∠P,
∴AF=PF,
∴AB=PB,
设AB=PB=x,PF=y,
则在Rt△PBF中,由勾股定理可得y2=22+x2①,
又由切割线定理可得(y+2)2=x•2x=2x2②,
则可解得x=4
,y=6,
∴AO=
AB=2
.
 (1)证明:
(1)证明:如图,延长BF、AC交于点M,
∵BF⊥AB,∴FB是⊙O的切线,
又CF是⊙O的切线,
∴CF=BF,
∴∠FCB=∠FBC,
又AB为直径,
∴∠BCM=90°,
∴∠B+∠M=∠BCF+∠FCM=90°,
∴∠FCM=∠M,
∴CF=MF,
∴BF=MF,
∵CD∥MB,
∴
| CE |
| MF |
| AE |
| AF |
| ED |
| FB |
∴CE=ED,
即E是CD的中点;
(2)解:
∵BF=EF=2=FC=FM,
∴∠FCE=∠FEC=∠AED,
又CD⊥AB,
∴∠FAB+∠AED=∠ECF+∠P,
∴∠FAB=∠P,
∴AF=PF,
∴AB=PB,
设AB=PB=x,PF=y,
则在Rt△PBF中,由勾股定理可得y2=22+x2①,
又由切割线定理可得(y+2)2=x•2x=2x2②,
则可解得x=4
| 2 |
∴AO=
| 1 |
| 2 |
| 2 |
点评:本题主要考查切线的性质及平行线分线段成比例等知识,在(1)中构造△ABM证得F是BM的中点是解题的关键,在(2)中注意勾股定理和切割线定理的应用.

练习册系列答案
相关题目
在0,-1,-x,
a,3-x,
,
中,是单项式的有( )
| 1 |
| 3 |
| 1-x |
| 2 |
| 1 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |