题目内容
19.如果a+b=2$\sqrt{a}$+6$\sqrt{b}$-10,那么ab=9.分析 利用配方法将等式变形为两个非负数的和等于0的形式,再根据非负数的性质即可求解.
解答 解:∵a+b=2$\sqrt{a}$+6$\sqrt{b}$-10,
∴a-2$\sqrt{a}$+1+b-6$\sqrt{b}$+9=0,
∴($\sqrt{a}$-1)2+($\sqrt{b}$-3)2=0,
∴$\sqrt{a}$-1=0,$\sqrt{b}$-3=0,
∴a=1,b=9,
∴ab=1×9=9.
故答案为9.
点评 本题考查了配方法的应用,二次根式的性质,非负数的性质,将等式变形为($\sqrt{a}$-1)2+($\sqrt{b}$-3)2=0是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
9.下列各式的变形中,正确的是( )
| A. | x6÷x=x | B. | (x2-$\frac{1}{x}$)÷x=x-1 | C. | x2+x3=x5 | D. | x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$ |
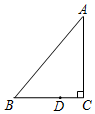 如图,Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.将△ABC绕点D按顺时针旋转角α(0<α<180°)后,如果点B恰好落在初始Rt△ABC的边上,那么α=120°.
如图,Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.将△ABC绕点D按顺时针旋转角α(0<α<180°)后,如果点B恰好落在初始Rt△ABC的边上,那么α=120°.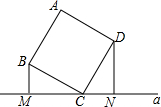 如图,正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的面积是5.
如图,正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的面积是5. 实数a、b在数轴上对应的如图所示,化简$\sqrt{a^2}$-$\sqrt{b^2}$+$\sqrt{{{({a-b})}^2}}$=-2a.
实数a、b在数轴上对应的如图所示,化简$\sqrt{a^2}$-$\sqrt{b^2}$+$\sqrt{{{({a-b})}^2}}$=-2a. 已知正方形纸 ABCD 的面积是 50cm 2,将四个角分别沿虚线往里折叠得到一个较小的正方形 EFGH ( E,F,G,H 分别为各边中点).
已知正方形纸 ABCD 的面积是 50cm 2,将四个角分别沿虚线往里折叠得到一个较小的正方形 EFGH ( E,F,G,H 分别为各边中点).