题目内容
7.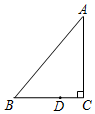 如图,Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.将△ABC绕点D按顺时针旋转角α(0<α<180°)后,如果点B恰好落在初始Rt△ABC的边上,那么α=120°.
如图,Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.将△ABC绕点D按顺时针旋转角α(0<α<180°)后,如果点B恰好落在初始Rt△ABC的边上,那么α=120°.
分析 作出图形,根据旋转的性质可得B′D=BD,然后解直角三角形求出∠B′DC,然后根据平角等于180°求出∠BDB′,即可得解.
解答  解:如图,∵△ABC绕着点D顺时针旋转α度后得到△A′B′C′,
解:如图,∵△ABC绕着点D顺时针旋转α度后得到△A′B′C′,
∴B′D=BD,
∵BD=2CD,
∴B′D=2CD,
在Rt△B′CD中,sin∠B′DC=$\frac{CD}{B′D}$=$\frac{CD}{2CD}$=$\frac{1}{2}$,
∴∠B′DC=60°,
∴∠BDB′=180°-60°=120°,
即旋转角α=120°.
故答案为:120.
点评 本题考查了旋转的性质,解直角三角形,利用锐角的正弦值求出∠B′DC是解题的关键,作出图形更形象直观.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若抛物线y=x2-2x-1与x轴的一个交点坐标为(m,0),则代数式m2-2m+2017的值为( )
| A. | 2019 | B. | 2018 | C. | 2016 | D. | 2015 |
 如图,三角形ABE向右平移一定距离后得到三角形CDF,若∠BAE=60°,∠B=25°,则∠ACD=25°.
如图,三角形ABE向右平移一定距离后得到三角形CDF,若∠BAE=60°,∠B=25°,则∠ACD=25°. 如图,正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,求FM的长.
如图,正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,求FM的长.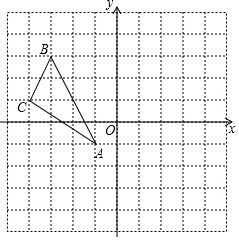 如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.