题目内容
制造一种产品,原来每件的成本是300元,由于连续两次降低成本,现在每件的成本是192元.若两次降低成本的百分率相同.求第一次降低成本后每件的售价是多少元?
考点:一元二次方程的应用
专题:增长率问题
分析:利用等量关系:原来的成本×(1-降低的百分率)2=192,列出方程求得降低成本的百分率,再进一步求得答案.
解答:解:解:设平均每次降低成本的百分率为x,
300×(1-x)2=192,
解得:x1=0.2,x2=1.8(不合题意,舍去),
第一次降低成本后每件的售价300×(1-20%)=240元.
答:第一次降低成本后每件的售价是240元.
300×(1-x)2=192,
解得:x1=0.2,x2=1.8(不合题意,舍去),
第一次降低成本后每件的售价300×(1-20%)=240元.
答:第一次降低成本后每件的售价是240元.
点评:考查一元二次方程的应用;求平均变化率的方法为:若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
计算(-2)-3的结果等于( )
| A、-1 | B、-5 | C、5 | D、1 |
借助一副三角尺,你能画出的角的度数是( )
| A、65° | B、15° |
| C、85° | D、95° |
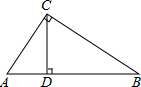 在Rt△ABC中,∠ACB=90°,CD⊥AB,
在Rt△ABC中,∠ACB=90°,CD⊥AB,