题目内容
如图，在?ABCD中，E是BC边上的一点，且BE：EC=2：1，延长AE交DC延长线于点F，则AB：DF=考点：相似三角形的判定与性质,平行四边形的性质
专题：
分析：根据平行四边形的对边相等，得△ABE∽△FCE，AB=CD，由相似三角形的对应边成比例来求AB：DF的值．
解答：解：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∴△ABE∽△FCE，
∴AB：FC=BE：EC=2：1，
∴AB：DF=AB：（AB+CF）=2：3，
故答案是：2：3．
∴AB∥CD，AB=CD，
∴△ABE∽△FCE，
∴AB：FC=BE：EC=2：1，
∴AB：DF=AB：（AB+CF）=2：3，
故答案是：2：3．
点评：本题考查了相似三角形的判定与性质、平行四边形的性质．三角形相似的判定一直是中考考查的热点之一，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边，对顶角相等等隐含条件．
练习册系列答案
相关题目
如图，△ABC中，外角∠CBD和外角∠BCE的平分线BF，CF交于点F．求证：点F到三边AC，AB，BC所在直线的距离相等．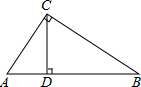
在Rt△ABC中，∠ACB=90°，CD⊥AB，