题目内容
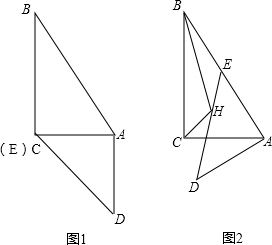 已知如图1,Rt△ABC和Rt△ADE的直角边AC和AE重叠在一起,AD=AE,∠B=30°,∠DAE=∠ACB=90°.
已知如图1,Rt△ABC和Rt△ADE的直角边AC和AE重叠在一起,AD=AE,∠B=30°,∠DAE=∠ACB=90°.(1)如图1,填空:∠BAD=
| BC |
| CD |
(2)如图2,将△ADE绕点A顺时针旋转,使AE到AB边上,∠ACH=∠BCH,连接BH,则H点是否为三角形ABC内切圆的圆心,为什么?
考点:旋转的性质,三角形的内切圆与内心
专题:计算题
分析:(1)如图1,利用互余计算出∠BAC=60°,根据含30度的直角三角形三边的关系得BC=
AC,则判断△ADE为等腰直角三角形,得到CD=
AC,于是∠BAD=∠BAC+∠CAD=150°,可计算出
=
;
(2)连结CE、AH,如图2,根据旋转的性质得AD=AC=AE,∠AED=∠D=45°,加上∠EAC=60°,则可判断△ACE为等边三角形,得到∠AEC=∠ACE=45°,于是可计算出∠HEC=∠HCE=15°,得到HE=HC,接着可证明△AHE≌△AHC,得到∠HAE=∠HAC,即AH为∠CAB的平分线,加上CH平分∠ACB,所以点H为△ABC的角平分线的交点,于是根据三角形内心的定义可判断H点为三角形ABC内切圆的圆心.
| 3 |
| 2 |
| BC |
| CD |
| ||
| 2 |
(2)连结CE、AH,如图2,根据旋转的性质得AD=AC=AE,∠AED=∠D=45°,加上∠EAC=60°,则可判断△ACE为等边三角形,得到∠AEC=∠ACE=45°,于是可计算出∠HEC=∠HCE=15°,得到HE=HC,接着可证明△AHE≌△AHC,得到∠HAE=∠HAC,即AH为∠CAB的平分线,加上CH平分∠ACB,所以点H为△ABC的角平分线的交点,于是根据三角形内心的定义可判断H点为三角形ABC内切圆的圆心.
解答: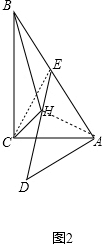 解:(1)如图1,∵∠B=30°,∠ACB=90°,
解:(1)如图1,∵∠B=30°,∠ACB=90°,
∴∠BAC=60°,BC=
AC,
∵AD=AE,∠DAE=90°,
∴△ADE为等腰直角三角形,
∴CD=
AC,
∴∠BAD=∠BAC+∠CAD=150°,
=
=
,
故答案为150°,
;
(2)H点是三角形ABC内切圆的圆心.理由如下:
连结CE、AH,如图2,
∵∠ACH=∠BCH,
∴∠ACH=45°,
∵△ADE绕点A顺时针旋转,使AE到AB边上,
∴AD=AC=AE,∠AED=∠D=45°,
而∠EAC=60°,
∴△ACE为等边三角形,
∴∠AEC=∠ACE=45°,
∴∠HEC=∠HCE=15°,
∴HE=HC,
在△AHE和△AHC中,
,
∴△AHE≌△AHC(SSS),
∴∠HAE=∠HAC,
∴AH为∠CAB的平分线,
而CH平分∠ACB,
∴点H为△ABC的角平分线的交点,
∴H点是三角形ABC内切圆的圆心.
 解:(1)如图1,∵∠B=30°,∠ACB=90°,
解:(1)如图1,∵∠B=30°,∠ACB=90°,∴∠BAC=60°,BC=
| 3 |
∵AD=AE,∠DAE=90°,
∴△ADE为等腰直角三角形,
∴CD=
| 2 |
∴∠BAD=∠BAC+∠CAD=150°,
| BC |
| CD |
| ||
|
| ||
| 2 |
故答案为150°,
| ||
| 2 |
(2)H点是三角形ABC内切圆的圆心.理由如下:
连结CE、AH,如图2,
∵∠ACH=∠BCH,
∴∠ACH=45°,
∵△ADE绕点A顺时针旋转,使AE到AB边上,
∴AD=AC=AE,∠AED=∠D=45°,
而∠EAC=60°,
∴△ACE为等边三角形,
∴∠AEC=∠ACE=45°,
∴∠HEC=∠HCE=15°,
∴HE=HC,
在△AHE和△AHC中,
|
∴△AHE≌△AHC(SSS),
∴∠HAE=∠HAC,
∴AH为∠CAB的平分线,
而CH平分∠ACB,
∴点H为△ABC的角平分线的交点,
∴H点是三角形ABC内切圆的圆心.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形和等腰直角三角形的性质、三角形内切圆的圆心.

练习册系列答案
相关题目
若关于x的方程(a-1)x+1=0是一元一次方程,则( )
| A、a≠0 | B、a≠1 |
| C、a为任意有理数 | D、以上都不对 |
已知函数y=x2-2015x+2014与x轴交点是(m,0),(n,0),则(m2-2014m+2014)(n2-2014n+2014)的值是( )
| A、2013 | B、2014 |
| C、2015 | D、2016 |
等腰三角形的两个外角的度数比为1:4,则它的底角的度数是( )
| A、140° | B、20° |
| C、60°或140° | D、60° |
 如图,已知点A(-4,4),点B为x轴的负半轴上的点,C为函数y=
如图,已知点A(-4,4),点B为x轴的负半轴上的点,C为函数y= 已知:如图,直线l:y=-x-1,一组可由平移变换得到的抛物线的顶点为B1,B2、B3、…Bn(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0)(n为正整数),其中x1=0,x2=2,则x3=
已知:如图,直线l:y=-x-1,一组可由平移变换得到的抛物线的顶点为B1,B2、B3、…Bn(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0)(n为正整数),其中x1=0,x2=2,则x3=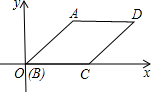 如图,?ABCD放入直角坐标系,BC在x轴上,且AB=4,BC=3,∠ABC=45°,则点D的坐标为
如图,?ABCD放入直角坐标系,BC在x轴上,且AB=4,BC=3,∠ABC=45°,则点D的坐标为