题目内容
19.已知关于x的一元二次方程x2-2(1-k)x+k2=0的两个实数根为x1,x2.(1)求k的取值范围;
(2)设y=x1+x2,当y取最小值时,求相应k的值,并求出最小值.
分析 (1)由于关于x的一元二次方程x2-2(1-k)x+k2=0有两个实数根,可知△≥0,据此进行计算即可;
(2)由根与系数的关系得出y=-2k+2,进一步利用函数的性质,结合k的取值求得答案即可.
解答 解:(1)∵关于x的一元二次方程x2-2(1-k)x+k2=0的两个实数根为x1,x2,
∴△=[-2(1-k)]2-4k2 =4-8k≥0,
∴k≤$\frac{1}{2}$;
(2)y=x1+x2=2(1-k)=-2k+2,
∵-2<0,
∴y随着x的增大而减小,当k取得最大值时,y值最小,
∵k≤$\frac{1}{2}$,
∴当k=$\frac{1}{2}$时,y最小=-2×$\frac{1}{2}$+2=1.
点评 本题考查了根的判别式,要知道一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.以及一次函数的性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
4.关于x的方程ax2+2x-1=0有实数根,则a的取值范围正确的是( )
| A. | a>-1 | B. | a≥-1 | C. | a≤-1 | D. | a≥-1且a≠0 |
11.气象台预报“我市明天的降雨概率是90%”,对此信息说法正确的是( )
| A. | 我市明天有90%的地区降雨 | B. | 我市明天将有90%的时间降雨 | ||
| C. | 我市明天会降90%的雨水 | D. | 我市明天降雨的可能性较大 |
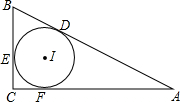 如图,⊙I是直角△ABC的内切圆,切点为D、E、F,若AF=10,BE=3,则△ABC的面积为30.
如图,⊙I是直角△ABC的内切圆,切点为D、E、F,若AF=10,BE=3,则△ABC的面积为30.