题目内容
17．已知抛物线y=2x2+m2-2m．（1）若抛物线过原点，则m=0或2；
（2）若抛物线的最小值为-1，则m=1．
分析 （1）把原点坐标代入可得到关于m的方程，可求得m的值；
（2）由抛物线解析式可求得抛物线的最小值，由条件可得到关于m的方程，可求得m的值．
解答 解：
（1）当抛物线过原点时，则坐标（0，0）满足函数解析式，
∴m2-2m=0，解得m=0或m=2，
故答案为：0或2；
（2）∵y=2x2+m2-2m，
∴抛物线最小值为m2-2m，
∵抛物线的最小值为-1，
∴m2-2m=-1，解得m1=m2=1，
故答案为：1．
点评 本题主要考查二次函数图象上点的坐标特征，掌握函数图象上的点的坐标满足函数解析式是解题的关键．
练习册系列答案
相关题目
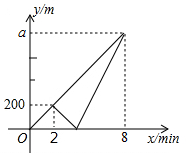周末，小明和弟弟从家出发，步行去吉林省图书馆学习．出发2分钟后，小明发现弟弟的数学书忘记带了，弟弟继续按原速前往图书馆，小明按原路原速返回家取书，然后骑自行前往图书馆，恰好与弟弟同时到达图书馆．小明和弟弟各自距家的路程y（m）与小明步行的时间x（min）之间的函数图象如图所示．
如图，已知AB∥CD，GH平分∠EGB，MN平分∠EMD，求证：GH∥MN．