题目内容
 如图,已知:AD∥BC,∠EAC=2∠C,BD平分∠ABC,AC=4cm,求AD长.
如图,已知:AD∥BC,∠EAC=2∠C,BD平分∠ABC,AC=4cm,求AD长.考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:根据三角形的一个外角等于与它不相邻的两个内角的和求出∠EAC=∠ABC+∠C,然后求出∠ABC=∠C,根据等角对等边可得AB=AC,根据角平分线的定义可得∠ABD=∠CBD,再根据两直线平行,内错角相等可得∠CBD=∠D,然后求出∠ABD=∠D,再利用等角对等边可得AD=AB,从而得解.
解答:解:由三角形的外角性质得,∠EAC=∠ABC+∠C,
∵∠EAC=2∠C,
∴∠ABC=∠C,
∴AB=AC=4cm,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵AD∥BC,
∴∠CBD=∠D,
∴∠ABD=∠D,
∴AD=AB=4cm.
∵∠EAC=2∠C,
∴∠ABC=∠C,
∴AB=AC=4cm,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵AD∥BC,
∴∠CBD=∠D,
∴∠ABD=∠D,
∴AD=AB=4cm.
点评:本题考查了等腰三角形的判定与性质,平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
有2张边长为a的正方形纸片,6张边长为a,b的长方形纸片,10张边长为b的正方形纸片,从中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼出一个大的正方形(无空隙,无重叠地拼接)则拼出的正方形的边长最长可以为( )
| A、a+3b | B、3a+b |
| C、2a+2b | D、2a+3b |
在△ABC中,AB=AC,那么在这个三角形中,三线重合的线段是( )
| A、∠A的平分线,AB边上的中线,AB边上的高 |
| B、∠A的平分线,BC边上的中线,BC边上的高 |
| C、∠B的平分线,AC边上的中线,AC边上的高 |
| D、∠C的平分线,AB边上的中线,AB边上的高 |
 如图,已知⊙O1和⊙O2相交于点A、B,O1在⊙O2上,AC是⊙O1的直径,连接CB并延长,与⊙O2相交于点D,连结AD.
如图,已知⊙O1和⊙O2相交于点A、B,O1在⊙O2上,AC是⊙O1的直径,连接CB并延长,与⊙O2相交于点D,连结AD.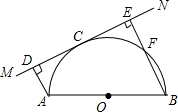 如图,已知AB为半圆O的直径,直线MN切半圆于点C,AD⊥MN于点D,BE⊥MN于点E,BE交半圆于点F,AD=3cm,BE=7cm.
如图,已知AB为半圆O的直径,直线MN切半圆于点C,AD⊥MN于点D,BE⊥MN于点E,BE交半圆于点F,AD=3cm,BE=7cm.