题目内容
 如图,已知⊙O1和⊙O2相交于点A、B,O1在⊙O2上,AC是⊙O1的直径,连接CB并延长,与⊙O2相交于点D,连结AD.
如图,已知⊙O1和⊙O2相交于点A、B,O1在⊙O2上,AC是⊙O1的直径,连接CB并延长,与⊙O2相交于点D,连结AD.(1)求证:AD是⊙O2的直径.
(2)求证:DA=DC.
考点:相交两圆的性质
专题:证明题
分析:(1)首先连接AB,由AC是⊙O1的直径,根据直径所对的圆周角是直角,可得∠ABC=90°,又由90°的圆周角所对的弦是直径,即可证得AD是⊙O2的直径;
(2)连结O1O2,根据三角形的中位线定理证得O1O2∥CD从而证得∠C=∠AO1O2,根据等边对等角求得∴∠O2AO1=∠AO1O2,进而求得∠C=∠O1AO2,即可证得结论.
(2)连结O1O2,根据三角形的中位线定理证得O1O2∥CD从而证得∠C=∠AO1O2,根据等边对等角求得∴∠O2AO1=∠AO1O2,进而求得∠C=∠O1AO2,即可证得结论.
解答: 证明:(1)连结AB
证明:(1)连结AB
∵AC是⊙O1的直径
∴∠ABC=90°
∴∠ABD=90°,AD是⊙O2的直径
(2)连结O1O2
∵AO1=O1C,AO2=O2D,
∴O1O2∥CD
∴∠C=∠AO1O2
又∵O2A=O1O2
∴∠O2AO1=∠AO1O2
∴DA=DC.
 证明:(1)连结AB
证明:(1)连结AB∵AC是⊙O1的直径
∴∠ABC=90°
∴∠ABD=90°,AD是⊙O2的直径
(2)连结O1O2
∵AO1=O1C,AO2=O2D,
∴O1O2∥CD
∴∠C=∠AO1O2
又∵O2A=O1O2
∴∠O2AO1=∠AO1O2
∴DA=DC.
点评:此题考查了圆周角定理以及三角形中位线线的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
-
的相反数是( )
| 1 |
| 8 |
| A、-8 | ||
B、
| ||
| C、0.8 | ||
| D、8 |
 观察图,它可以看成是由哪几个基本图形经过怎样的变换产生的?请用学过的平移、旋转、轴对称变化来分析这个图形的形成过程.
观察图,它可以看成是由哪几个基本图形经过怎样的变换产生的?请用学过的平移、旋转、轴对称变化来分析这个图形的形成过程.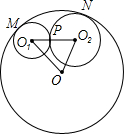 如图,⊙O1和⊙O2外切于P,并且⊙O和⊙O1、⊙O2分别内切于M、N,△O1O2O的周长为18cm.求⊙O的半径长.
如图,⊙O1和⊙O2外切于P,并且⊙O和⊙O1、⊙O2分别内切于M、N,△O1O2O的周长为18cm.求⊙O的半径长.
 如图,平面内有公共端点的五条射线OA、OB、OC、OD、OE,从射线OA开始,在射线上写出数字1,2,3,4,5,6,7,8,9,10,…按此规律,则“2014”在射线
如图,平面内有公共端点的五条射线OA、OB、OC、OD、OE,从射线OA开始,在射线上写出数字1,2,3,4,5,6,7,8,9,10,…按此规律,则“2014”在射线 如图,已知:AD∥BC,∠EAC=2∠C,BD平分∠ABC,AC=4cm,求AD长.
如图,已知:AD∥BC,∠EAC=2∠C,BD平分∠ABC,AC=4cm,求AD长.