题目内容
如图，已知EF∥CD，DG交AC于点G，∠1=∠2，试判断∠AGD与∠ACB的关系，并说明理由．考点：平行线的判定与性质
专题：计算题
分析：∠AGD=∠ACB，理由为：由EF与CD平行，利用两直线平行同位角相等得到一对角相等，与已知角相等等量代换得到一对内错角相等，利用内错角相等两直线平行即可得证．
解答：解：∠AGD=∠ACB，理由为：
∵EF∥CD，
∴∠2=∠3，
∵∠1=∠2，
∴∠1=∠3，
∴DG∥BC，
∴∠AGD=∠ACB．
∵EF∥CD，
∴∠2=∠3，
∵∠1=∠2，
∴∠1=∠3，
∴DG∥BC，
∴∠AGD=∠ACB．
点评：此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关键．
练习册系列答案
相关题目
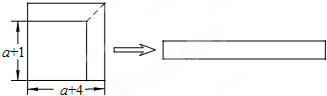
如图，从边长为（a+4）的正方形纸片中剪去一个边长为（a+1）的正方形（a＞0），剩余部分沿虚线又剪拼成一个长方形（不重叠、无缝隙），若拼成的长方形一边的长为3，则另一边的长为（ ）
| A、2a+5 | B、2a+8 |
| C、2a+3 | D、2a+2 |
