题目内容
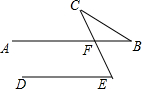
8. 五一节,某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观,并测量其高度.如图,塔身BD与地面垂直,他们先在A处测得塔顶端点D的仰角为45°,再沿着BA的方向后退16cm至C处,测得塔顶端点D的仰角为30°,求“海春轩塔”BD的高度.($\sqrt{3}$≈1.73,结果保留一位小数)
五一节,某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观,并测量其高度.如图,塔身BD与地面垂直,他们先在A处测得塔顶端点D的仰角为45°,再沿着BA的方向后退16cm至C处,测得塔顶端点D的仰角为30°,求“海春轩塔”BD的高度.($\sqrt{3}$≈1.73,结果保留一位小数)
分析 先根据题意得出∠BAD、∠BCD的度数及AC的长,再在Rt△ABD中可得出AB=BD,利用锐角三角函数的定义可得出BD的长.
解答 解:根据题意可知:
∠BAD=45°,∠BCD=30°,AC=12m.
在Rt△ABD中,
∵∠BAD=∠BDA=45°,
∴AB=BD.
在Rt△BDC中,
∵tan∠BCD=$\frac{BD}{BC}$,
∴$\frac{BD}{BC}$=$\frac{\sqrt{3}}{3}$,
则BC=$\sqrt{3}$BD,
又∵BC-AB=AC,
∴$\sqrt{3}$BD-BD=16,
解得:BD=8$\sqrt{3}$+8.
答:古塔BD的高度为(8$\sqrt{3}$+8)米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,涉及到等腰直角三角形的判定与性质、锐角三角函数的定义及特殊角的三角函数值,熟练掌握以上知识是解答此题的关键.

练习册系列答案
相关题目
 如图所示,一个宽度相等的纸条按如图所示方法折叠一下,则∠1=55°.
如图所示,一个宽度相等的纸条按如图所示方法折叠一下,则∠1=55°.
 如图,AB∥DE,∠E=60°,则∠B+∠C=60°.
如图,AB∥DE,∠E=60°,则∠B+∠C=60°.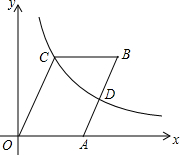 如图,?OABC的顶点B、C在第一象限,点A的坐标为(3,0),D为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点C、D两点,若∠COA=60°,则k的值为4$\sqrt{3}$.
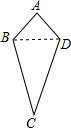
如图,?OABC的顶点B、C在第一象限,点A的坐标为(3,0),D为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点C、D两点,若∠COA=60°,则k的值为4$\sqrt{3}$. 研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;
研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;