题目内容
15.如图1,⊙O是△ABC的外接圆,AP是⊙O的切线.已知AC=4,BC=5.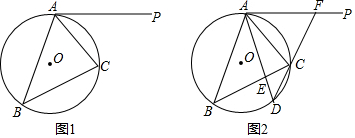
(1)求证:∠PAC=∠ABC;
(2)作∠BAC的平分线,与⊙O相交于点D,与BC相交于点E,连接并延长DC,与AP相交于点F(如图2),若AE=AC,求CF的长.
分析 (1)作直径AQ,连接QC,根据切线的性质得出∠PAQ=90°,求出∠PAC+∠CAQ=90°,根据圆周角定理得出∠ACQ=90°,∠PAC=∠Q,即可求出答案;
(2)求出∠AEC=∠ACE,∠FAC=∠ABC,根据相似三角形的判定得出△FAC∽△ABC,得出比例式,代入求出即可.
解答 (1)证明: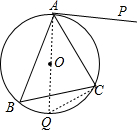
作直径AQ,连接QC,
∵AP是⊙O的切线,
∴∠PAQ=90°,
∴∠PAC+∠CAQ=90°,
∵AQ是直径,
∴∠ACQ=90°,
∴∠CAQ+∠Q=90°,
∴∠PAC=∠Q,
∵∠Q=∠ABC,
∴∠PAC=∠ABC;
(2)解:∵AD是∠BAC的平分线,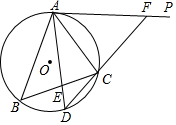
∴∠BAD=∠CAD,
∴∠ACF=∠ADC+∠CAD=∠ABC+∠BAD=∠AEC,
∵AE=AC,
∴∠AEC=∠ACE,
由(1)知:∠FAC=∠ABC,
∴△FAC∽△ABC,
∴$\frac{CF}{AC}$=$\frac{AC}{BC}$,
即$\frac{CF}{4}$=$\frac{4}{5}$,
∴CF=$\frac{16}{5}$.
点评 本题考查了切线的性质,圆周角定理,相似三角形的性质和判定,能灵活运用定理进行推理是解此题的关键,题目比较好,难度适中.

练习册系列答案
相关题目
19.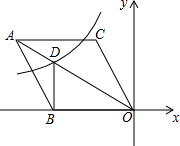 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-$\sqrt{3}$,3),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
10. 如图,在菱形ABCD中,点P是BC边上一动点,连结AP,AP的垂直平分线交BD于点G,交AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )
如图,在菱形ABCD中,点P是BC边上一动点,连结AP,AP的垂直平分线交BD于点G,交AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )
 如图,在菱形ABCD中,点P是BC边上一动点,连结AP,AP的垂直平分线交BD于点G,交AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )
如图,在菱形ABCD中,点P是BC边上一动点,连结AP,AP的垂直平分线交BD于点G,交AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )| A. | 变大 | B. | 先变大后变小 | C. | 先变小后变大 | D. | 不变 |
4.下列计算结果等于a5的是( )
| A. | a3+a2 | B. | a3•a2 | C. | (a3)2 | D. | a10÷a2 |
5.因式分解x2y-4y的结果是( )
| A. | y(x2-4) | B. | y(x-2)2 | C. | y(x+4)(x-4) | D. | y(x+2)(x-2) |
 某商家为了给新产品作宜传,向全社会征集广告用语及商标图案,结果如图所示的商标(图中阴影部分)中标,求此商标图案的面积.(虚线左边为扇形,右边为长方形)
某商家为了给新产品作宜传,向全社会征集广告用语及商标图案,结果如图所示的商标(图中阴影部分)中标,求此商标图案的面积.(虚线左边为扇形,右边为长方形)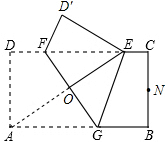 如图,矩形纸片ABCD中,AD=1,AB=2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.当△AED的外接圆与BC相切于BC的中点N.则折痕FG的长为$\frac{17}{15}$.
如图,矩形纸片ABCD中,AD=1,AB=2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.当△AED的外接圆与BC相切于BC的中点N.则折痕FG的长为$\frac{17}{15}$.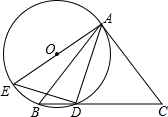 如图,在△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A、B、D三点作⊙O,AE是⊙O的直径,连接DE.
如图,在△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A、B、D三点作⊙O,AE是⊙O的直径,连接DE.