题目内容
13．若小李同学掷出的铅球在场地航砸出一个直径为10厘米，深2厘米的小坑，则该铅球的直径为（ ）| A． | 20厘米 | B． | 19.5厘米 | C． | 14.5厘米 | D． | 10厘米 |
分析 根据题意，把实际问题抽象成几何问题，即圆中与弦有关的问题，根据垂径定理，构造直角三角形，小坑的直径就是圆中的弦长，小坑的深就是拱高，利用勾股定理，设出未知数，列出方程，即可求出铅球的直径．
解答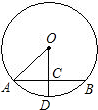 
解：根据题意，画出图形如图所示，
由题意知，AB=10厘米，CD=2厘米，OD是半径，且OC⊥AB，
∴AC=CB=5厘米，
设铅球的半径为r，则OC=r-2，
在Rt△AOC中，根据勾股定理，OC2+AC2=OA2，
即（r-2）2+52=r2，
解得：r=7.25，
所以铅球的直径为：2×7.25=14.5（厘米）．
故选：C．
点评 本题考查了垂径定理的应用和勾股定理．解决与弦有关的问题时，往往需构造以半径、弦心距和弦长的一半为三边的直角三角形，若设圆的半径为r，弦长为a，这条弦的弦心距为d，则有等式r2=d2+（$\frac{a}{2}$）2成立，知道这三个量中的任意两个，就可以求出另外一个．
练习册系列答案
相关题目
如图是一个几何体的俯视图，正方形中的数字是该位置上的小立方体数量，请画出从正面和左面看到的图形．
1．下列各式正确的是（ ）
| A． | 2+$\sqrt{2}$=2$\sqrt{2}$ | B． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C． | $\sqrt{27}$÷$\sqrt{3}$=3 | D． | $\sqrt{4}$=±2 |
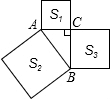如图，已知△ABC中，∠ACB=90°，以△ABC的各边为边在△ABC外作三个正方形，S1、S2、S3分别表示这三个正方形的面积．若S1=81，S2=225，则S3=144．
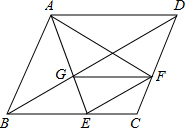如图，在?ABCD中，点E、F分别在BC、CD上，BE=DF，∠BAF=∠DAE．