题目内容
9．一个不透明的布袋里装有4个只有颜色不同的球，其中3个白球，1个红球．从中摸出1个球，记下颜色后放回搅匀，再摸出1个球．则两次都摸出红球的概率是$\frac{1}{16}$．分析 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次都摸出红球的情况，再利用概率公式即可求得答案．
解答 解：画树状图得：
∵共有16种等可能的结果，两次都摸出红球的只有1种情况，
∴两次都摸出红球的概率是：$\frac{1}{16}$．
故答案为：$\frac{1}{16}$．
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
名校课堂系列答案
相关题目
17．2014年成都市的国民生产总值为1034亿元，1034亿元用科学记数法表示正确的是（ ）
| A． | 1034×108元 | B． | 1.034×1011元 | C． | 1.0×1011元 | D． | 1.034×1012元 |
4．|-$\sqrt{5}$|的值等于（ ）
| A． | $\sqrt{5}$ | B． | -$\sqrt{5}$ | C． | ±$\sqrt{5}$ | D． | $\frac{\sqrt{5}}{5}$ |
14．从长度分别为2、6、7、9的4条线段中任取3条作三角形的边，能组成三角形的概率为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
1．已知二次函数y=x2+1的图象上有一点P（1，2）．若将该抛物线平移后所得的二次函数表达式为y=x2-2x-1，则点P经过该次平移后的坐标为（ ）
| A． | （2，1） | B． | （2，-1） | C． | （1，-2） | D． | （0，5） |
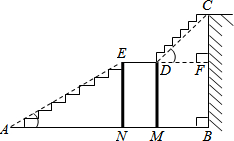如图是某宾馆大厅到二楼的楼梯设计图，已知BC=5米，AB=8米，DM、EN为平台的两根支柱，DM、EN垂直于AB，垂足分别为M、N，∠EAB=30°，∠CDF=45°．