题目内容
2. 如图,在△ABC中,DF∥AC,DE∥BC,求证:AE•CB=AC•CF.
如图,在△ABC中,DF∥AC,DE∥BC,求证:AE•CB=AC•CF.
分析 先根据DE∥BC得出△ADE∽△ABC,再由相似三角形的性质得出$\frac{AE}{AC}$=$\frac{DE}{CB}$,再由DF∥AC,DE∥BC得出四边形DEFC是平行四边形,进而可得出结论.
解答 证明:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AE}{AC}$=$\frac{DE}{CB}$.
∵DF∥AC,DE∥BC,
∴四边形DEFC是平行四边形,
∴DE=CF,
∴$\frac{AE}{AC}$=$\frac{CF}{CB}$,
∴AE•CB=AC•CF.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
相关题目
12.$\sqrt{16}$的平方根是( )
| A. | 4 | B. | -4 | C. | 2 | D. | ±2 |
14.5月29日,长沙地铁2号线试运营“满月”,根据“满月”报告,自4月29日12:30开门载客到5月28日20:00,地铁2号线共计运送乘客5330000人次,5330000这个数用科学记数法表示为( )
| A. | 533×104 | B. | 5.33×106 | C. | 53.3×105 | D. | 0.533×107 |
 如图,在△ABC中,∠B=50°,∠C=70°,∠CED=60°,求证:DE∥AB.
如图,在△ABC中,∠B=50°,∠C=70°,∠CED=60°,求证:DE∥AB.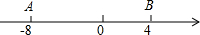 数轴上两个点A,B所对应的数为-8,4,A、B两点各自以一定的速度同时运动,且A点的运动速度为2个单位/秒.
数轴上两个点A,B所对应的数为-8,4,A、B两点各自以一定的速度同时运动,且A点的运动速度为2个单位/秒.