题目内容
10.如图所示,将斜边长为10cm,较短直角边为5cm的直角三角形绕较长直角边长为轴旋转一周得到一个圆锥,当圆锥中的内接圆柱的底面半径为$\frac{5}{2}$cm时,圆柱的侧面积有最大值,最大值为$\frac{25\sqrt{3}π}{2}$cm2.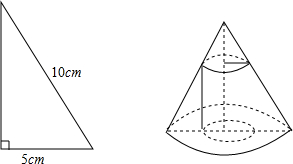
分析 设内接圆柱的底面半径为r,高为h,根据比例关系可用含r的式子表示h,再根据侧面积公式列出S关于r的函数解析式,根据二次函数性质可得其最值情况.
解答 解:由勾股定理可得直角三角形的另一条直角边为$\sqrt{1{0}^{2}-{5}^{2}}$=5$\sqrt{3}$,
设内接圆柱的底面半径为r,高为h,
由图可知,
$\frac{h}{5\sqrt{3}}$=$\frac{5-r}{5}$,
∴h=$\sqrt{3}$(5-r),
内接圆柱的侧面积S=2πr•h=2πr•$\sqrt{3}$(5-r)=-2$\sqrt{3}$π(r-$\frac{5}{2}$)2+$\frac{25\sqrt{3}π}{2}$,
∴当r=$\frac{5}{2}$cm时,圆柱的侧面积最大,最大面积为$\frac{25\sqrt{3}π}{2}$cm2,
故答案为:$\frac{5}{2}$,$\frac{25\sqrt{3}π}{2}$.
点评 本题主要考查二次函数的应用及圆柱侧面积的计算,根据比例式得出圆柱的高与底面半径的关系及熟练掌握函数性质是解题的关键.

练习册系列答案
相关题目
20.“-7+18-9-15“可以读成( )
| A. | -7,18,-9,-15的代数和 | B. | -7加18减-9减15 | ||
| C. | -7加18加+9加+15 | D. | -7减18减9减-15 |
1.正整数a、b满足a+b≤10,则ab>20的概率为( )
| A. | $\frac{5}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{11}$ |
18.在二次函数y=ax2+bx+c(a≠0)中,已知b2=ac,且当x=0时y=-4,则下列说法正确的是( )
| A. | 抛物线开口向上 | B. | 抛物线与y轴交于正半轴 | ||
| C. | 抛物线与x轴有两个交点 | D. | y有最大值,为-3 |
19.下列事件属于必然事件的是( )
| A. | 明天一定不下雨 | |
| B. | 一个袋中装有5个红球,从中摸出一个是红球 | |
| C. | 购买1张彩票,中奖 | |
| D. | 随意翻到一本书的某项,这页的页码是奇数 |
 如图,在△ABC中,DF∥AC,DE∥BC,求证:AE•CB=AC•CF.
如图,在△ABC中,DF∥AC,DE∥BC,求证:AE•CB=AC•CF.