题目内容
3. 如图,已知AB∥ED,AB=ED,AF=DC.求证:∠EFD=∠BCA.
如图,已知AB∥ED,AB=ED,AF=DC.求证:∠EFD=∠BCA.
分析 根据平行线的性质可得∠EDC=∠FAB,再利用等式的性质证明AC=DF,然后可证明△ABC≌△DEF,根据全等三角形对应角相等可得结论:∠EFD=∠BCA.
解答 证明:∵AB∥ED,
∴∠EDC=∠FAB,
∵AF=DC,
∴AF+FC=CD+FC,
即AC=DF,
在△ABC和△DEF中$\left\{\begin{array}{l}{AB=ED}\\{∠CAB=∠DE}\\{AC=DF}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴∠EFD=∠BCA.
点评 此题主要考查了全等三角形的判定和性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
 如图,正方形ABCD的对角线AC,BD相交于点O.DF∥AC,CF∥DB,DF,CF相交于点F.问四边形OCFD是什么样的四边形?
如图,正方形ABCD的对角线AC,BD相交于点O.DF∥AC,CF∥DB,DF,CF相交于点F.问四边形OCFD是什么样的四边形?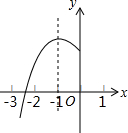 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论: 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点B,点C为y轴上一点,且B是线段OC的中点.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点B,点C为y轴上一点,且B是线段OC的中点. 如图所示,∠AOB=45°,OP平分∠AOB,PC∥OB,PD⊥OB,如果PC=6,那么PD=3$\sqrt{2}$.
如图所示,∠AOB=45°,OP平分∠AOB,PC∥OB,PD⊥OB,如果PC=6,那么PD=3$\sqrt{2}$. 已知:如图,AB=AE,∠1=∠2,∠B=∠E,求证:BC=DE.
已知:如图,AB=AE,∠1=∠2,∠B=∠E,求证:BC=DE. 如图,在平面直角坐标系总,直线y=kx+b经过第一象限的点A(1,2)和点B(m,n)(m>1),且mn=2,过点B作BC⊥y轴,垂足为C,△ABC的面积为2.
如图,在平面直角坐标系总,直线y=kx+b经过第一象限的点A(1,2)和点B(m,n)(m>1),且mn=2,过点B作BC⊥y轴,垂足为C,△ABC的面积为2.