题目内容
已知tanα=3，计算（1）（sinα+cosα）2；（2）
的值．
| 4sinα-2cosα |
| 5cosα+3sinα |
考点：解直角三角形,勾股定理,锐角三角函数的定义
专题：计算题
分析：（1）利用tanα=
=3得到a=3b，利用勾股定理求得斜边c=
b，代入即可得到答案；
（2）分子分母同时除以cosα，把tanα=3代入答案可得；
| a |
| b |
| 10 |
（2）分子分母同时除以cosα，把tanα=3代入答案可得；
解答：解：（1）∵tanα=
=3，
∴a=3b，
∴c=
=
b，
∴（sinα+cosα）2=（
+
）2=（
+
） 2=
；
（2）∵tanα=
=3，
∴tanα=
=3，
=
=
=
．
| a |
| b |
∴a=3b，
∴c=
| a2+b2 |
| 10 |
∴（sinα+cosα）2=（
| a |
| c |
| b |
| c |
| 3b | ||
|
| b | ||
|
| 8 |
| 5 |
（2）∵tanα=
| a |
| b |
∴tanα=
| sinα |
| cosα |
| 4sinα-2cosα |
| 5cosα+3sinα |
4
| ||||
5
|
| 4×3-2 |
| 5+3×3 |
| 5 |
| 7 |
点评：本题主要考查了三角函数的恒等变换应用，解题的关键是构造出tanα．
练习册系列答案
相关题目
如图所示，在平面直角坐标系中，0为坐标原点，⊙E过点O．与x轴、y轴分别交于B、A两点，点E坐标为（-2，2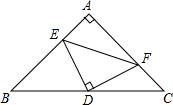
如图，在等腰Rt△ABC中，D是斜边BC的中点，E在边AB上，F在边AC上，且∠EDF=90°．