题目内容
19.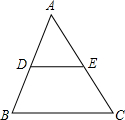 如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$=$\frac{1}{8}$.
如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$=$\frac{1}{8}$.
分析 先根据DE∥BC得出△ADE∽△ACB,由相似三角形的性质求出两个相似三角形的面积比,进而求出$\frac{{S}_{△ADE}}{{S}_{△四边形BCDE}}$的值.
解答 解:DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2=($\frac{AD}{AD+BD}$)2,
∵AD=1,DB=2,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}=\frac{1}{9}$,
∴$\frac{S△ADE}{{S}_{四边形BCED}}=\frac{{S}_{△ADE}}{{S}_{△ABC}-{S}_{△ADE}}=\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 本题主要考查了相似三角形的判定和性质,本题的关键是利用相似三角形的面积比等于相似比的平方求值.

练习册系列答案
相关题目
9. M,N是两个有理数,由图可知M,N所表示的数分别为( )
M,N是两个有理数,由图可知M,N所表示的数分别为( )
 M,N是两个有理数,由图可知M,N所表示的数分别为( )
M,N是两个有理数,由图可知M,N所表示的数分别为( )| A. | -2.5,2.5 | B. | -1.5,3.5 | C. | 2.5,-1.5 | D. | -1.5,2.5 |
14.如图,已知AB⊥GH,CD⊥GH,直线CD,EF,GH相交于一点O,若∠1=42°,则∠2等于( )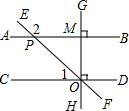

| A. | 130° | B. | 138° | C. | 140° | D. | 142° |
11.-8的立方根是( )
| A. | -2$\sqrt{2}$ | B. | ±2 | C. | 2 | D. | -2 |
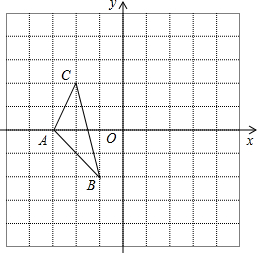 如图,小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,-2),B(3,-1),C(2,1).
如图,小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,-2),B(3,-1),C(2,1).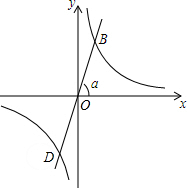 如图,正比例函数的图象与x轴正方向所成角为α,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B,D.
如图,正比例函数的图象与x轴正方向所成角为α,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B,D.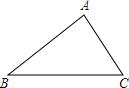 如图,在锐角三角形ABC中,AB=10,AC=2$\sqrt{13}$,sinB=$\frac{3}{5}$.
如图,在锐角三角形ABC中,AB=10,AC=2$\sqrt{13}$,sinB=$\frac{3}{5}$.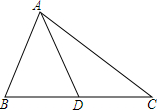 △ABC中,AB=AD,∠C=45°,AC=m,则BC+CD=$\sqrt{2}$m.
△ABC中,AB=AD,∠C=45°,AC=m,则BC+CD=$\sqrt{2}$m.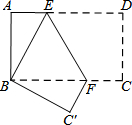 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.