题目内容
8.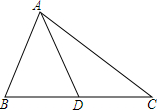 △ABC中,AB=AD,∠C=45°,AC=m,则BC+CD=$\sqrt{2}$m.
△ABC中,AB=AD,∠C=45°,AC=m,则BC+CD=$\sqrt{2}$m.
分析 过A作AE⊥BD于E,由于AB=AD,于是得到BE=DE,推出△AEC是等腰直角三角形,根据勾股定理得到AE=CE=$\frac{\sqrt{2}}{2}$m,即可得到结论.
解答  解:过A作AE⊥BD于E,
解:过A作AE⊥BD于E,
∵AB=AD,
∴BE=DE,
∵∠C=45°,
∴△AEC是等腰直角三角形,
∵AC=m,
∴AE=CE=$\frac{\sqrt{2}}{2}$m,
∴BC+CD=CD+DE+BE+CD=2CE=$\sqrt{2}$m,
故答案为:$\sqrt{2}$m.
点评 本题考查了等腰三角形的性质,等腰直角三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列图象中,表示直线y=-x+1的是( )
| A. |  | B. |  | C. |  | D. |  |
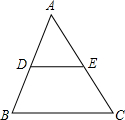 如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$=$\frac{1}{8}$.
如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$=$\frac{1}{8}$. “中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h(约为19.4m/s).如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方40m的C处(即AC=40m),过了2s后,行驶到B处,测得小汽车与车速检测仪间距离AB为50m,问:这辆小汽车超速了吗?
“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h(约为19.4m/s).如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方40m的C处(即AC=40m),过了2s后,行驶到B处,测得小汽车与车速检测仪间距离AB为50m,问:这辆小汽车超速了吗?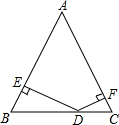 [问题提出]
[问题提出]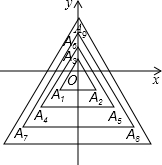 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们