题目内容
方程|x|-
=
的实数根的个数为( )
| 4 |
| |x| |
| 3|x| |
| x |
| A、1 | B、2 | C、3 | D、4 |
考点:解分式方程,绝对值
专题:
分析:首先分别从①当x>0时,原式变为:x-
=3与②当x<0时,原式变为:-x+
=-3去分析,利用分式方程的求解方法,即可求得答案.
| 4 |
| x |
| 4 |
| x |
解答:解:①当x>0时,原式变为:x-
=3,
方程的两边同乘x,得:x2-4=3x,
即x2-3x-4=0,
∴(x+1)(x-4)=0,
解得:x=-1(舍去),x=4.
检验:把x=4代入x=4≠0,即x=4是原分式方程的解;
②当x<0时,原式变为:-x+
=-3,
方程的两边同乘x,得:x2-3x-4=0,
∴(x+1)(x-4)=0,
解得:x=-1,x=4(舍去).
检验:把x=-1代入x=-1≠0,即x=-1是原分式方程的解;
∴方程|x|-
=
的实数根的个数为2个.
故选B.
| 4 |
| x |
方程的两边同乘x,得:x2-4=3x,
即x2-3x-4=0,
∴(x+1)(x-4)=0,
解得:x=-1(舍去),x=4.
检验:把x=4代入x=4≠0,即x=4是原分式方程的解;
②当x<0时,原式变为:-x+
| 4 |
| x |
方程的两边同乘x,得:x2-3x-4=0,
∴(x+1)(x-4)=0,
解得:x=-1,x=4(舍去).
检验:把x=-1代入x=-1≠0,即x=-1是原分式方程的解;
∴方程|x|-
| 4 |
| |x| |
| 3|x| |
| x |
故选B.
点评:此题考查了分式方程的求解方法以及绝对值的性质.此题难度适中,注意掌握分类讨论思想的应用是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
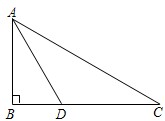 如图,某中学九年级数学兴趣小组测量校内旗杆AB高度,在C点测得旗杆顶端A的仰角为30°,向前走了26米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度忽略不计,点B、D、C在同一直线上),求旗杆AB的高度(结果保留3个有效数字,
如图,某中学九年级数学兴趣小组测量校内旗杆AB高度,在C点测得旗杆顶端A的仰角为30°,向前走了26米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度忽略不计,点B、D、C在同一直线上),求旗杆AB的高度(结果保留3个有效数字, 在面积为1的△ABC中,P为边BC上的中点,点Q在边AC上,且AQ=2QC,连接AP,BQ相交于点R,求:△ABR的面积?
在面积为1的△ABC中,P为边BC上的中点,点Q在边AC上,且AQ=2QC,连接AP,BQ相交于点R,求:△ABR的面积?