题目内容
14. 已知:如图,AD⊥BC,EF⊥BC,垂足为D,F,∠4=∠C.求证:∠1=∠2.
已知:如图,AD⊥BC,EF⊥BC,垂足为D,F,∠4=∠C.求证:∠1=∠2.
分析 先根据垂直的定义得∠ADF=∠EFC=90°,则可判断AD∥EF,根据平行线的性质得∠2=∠DAC,再根据平行线的判定方法,由∠4=∠C可得DG∥AC,则利用平行线的性质得∠1=∠DAC,然后根据等量代换即可得到结论.
解答 证明:∵AD⊥BC,EF⊥BC,
∴∠ADF=∠EFC=90°,
∴AD∥EF,
∴∠2=∠DAC,
又∵∠4=∠C,
∴DG∥AC,
∴∠1=∠DAC,
∴∠1=∠2.
点评 本题考查了平行线的判定与性质:平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.也考查了垂线的定义.

练习册系列答案
相关题目
5.若线段a,b,c组成直角三角形,则它们的比为( )
| A. | 2:3:4 | B. | 3:4:6 | C. | 4:6:7 | D. | 7:24:25 |
9.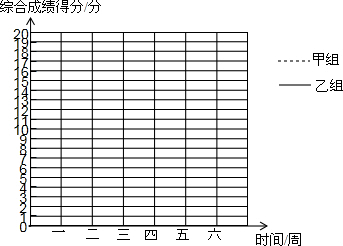 某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
(1)请根据上表中的数据完成下表;(注:方差的计算结果精确到0.1)
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图;
(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况做出简要评价.
 某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:| 周次 | ||||||
| 组别 | 一 | 二 | 三 | 四 | 五 | 六 |
| 甲组 | 12 | 15 | 16 | 14 | 14 | 13 |
| 乙组 | 9 | 14 | 10 | 17 | 16 | 18 |
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图;
(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况做出简要评价.
| 平均数 | 中位数 | 方差 | |
| 甲组 | 14 | 14 | 1.7 |
| 乙组 | 14 | 15 | 11.7 |
19.某校要从九(一)班和九(二)班中各选取10名女同学组成礼仪队,选取的两班女生的身高如下:(单位:厘米)
九(一)班:168 167 170 165 168 166 171 168 167 170
九(二)班:165 167 169 170 165 168 170 171 168 167
(1)补充完成下面的统计分析表:
(2)请选一个合适的统计量作为选择标准,说明哪一个班能被选取.
九(一)班:168 167 170 165 168 166 171 168 167 170
九(二)班:165 167 169 170 165 168 170 171 168 167
(1)补充完成下面的统计分析表:
| 班级 | 平均数 | 方差 | 中位数 |
| 一班 | 168 | 3.2 | 168 |
| 二班 | 168 | 3.8 | 168 |
6.两个相似三角形的对应边分别是15cm和25cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
| A. | 75cm,115cm | B. | 60cm,100cm | C. | 85cm,125cm | D. | 45cm,85cm |
3.在下列几张扑克牌中,牌面是中心对称图形的有( )个.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,OA,OB,OC,OD是⊙O的半径,
如图,OA,OB,OC,OD是⊙O的半径,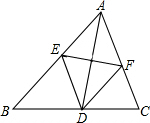 如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB、AC于点E、F.
如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB、AC于点E、F.