题目内容
20. 如图,在平面直角坐标系中,已知点A(9,12),点B是x轴正半轴上的一个动点,作AC⊥AB,使AC:AB=4:3,过点C的直线y=-$\frac{4}{3}$x$+\frac{4}{3}$m$+\frac{100}{3}$交x轴于点D,当m取何值时,△OCD为等腰三角形?
如图,在平面直角坐标系中,已知点A(9,12),点B是x轴正半轴上的一个动点,作AC⊥AB,使AC:AB=4:3,过点C的直线y=-$\frac{4}{3}$x$+\frac{4}{3}$m$+\frac{100}{3}$交x轴于点D,当m取何值时,△OCD为等腰三角形?
分析 过A作AE⊥OD于E,过C作CF⊥OD于F,AH⊥CF于H,则四边形AEFH是矩形,求得∠EAH=90°,推出△ABE∽△ACH,根据相似三角形的性质得到AE=12,OE=9,得到OF=25,CF=-$\frac{4}{3}$×25$+\frac{4}{3}$m$+\frac{100}{3}$=$\frac{4}{3}$m,根据勾股定理得到OC=$\sqrt{2{5}^{2}+\frac{16}{9}m}$,OD=m+25,CD=$\sqrt{{m}^{2}+\frac{16}{9}{m}^{2}}$,根据等腰三角形的定义列方程即可得到结论.
解答 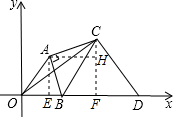 解:过A作AE⊥OD于E,过C作CF⊥OD于F,AH⊥CF于H,
解:过A作AE⊥OD于E,过C作CF⊥OD于F,AH⊥CF于H,
则四边形AEFH是矩形,
∴∠EAH=90°,
∵∠CAB=90°,
∴∠EAB=∠CAH,
∵∠AEB=∠AHC=90°,
∴△ABE∽△ACH,
∴$\frac{AE}{AH}=\frac{AB}{AC}$=$\frac{3}{4}$,
∵A(9,12),
∴AE=12,OE=9,
∴AH=16,
∴OF=25,
∴CF=-$\frac{4}{3}$×25$+\frac{4}{3}$m$+\frac{100}{3}$=$\frac{4}{3}$m,
∴OC=$\sqrt{C{F}^{2}+O{F}^{2}}$=$\sqrt{2{5}^{2}+\frac{16}{9}m}$,OD=m+25,CD=$\sqrt{{m}^{2}+\frac{16}{9}{m}^{2}}$,
当OC=OD时,$\sqrt{2{5}^{2}+\frac{16}{9}m}$=m+25,解得:m=$\frac{450}{7}$,
当OD=CD时,m+25=$\frac{5}{3}$m,解得:m=$\frac{75}{2}$,
当OC=CD时,$\sqrt{2{5}^{2}+\frac{16}{9}m}$=$\frac{5}{3}$m,解得:m=25,
综上所述:当m=$\frac{450}{7}$或$\frac{75}{2}$或25时,△OCD为等腰三角形.
点评 本题考查了一次函数图象上点的坐标特征,等腰三角形的判定,勾股定理,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

 快捷英语周周练系列答案
快捷英语周周练系列答案| A. | x2+2x-1=(x-1)2 | B. | x2+1=(x+1)2 | C. | 2x2-2=2(x+1)(x-1) | D. | x2-x+1=x(x-1)+1 |
 如图的伸缩门,其原理是( )
如图的伸缩门,其原理是( )| A. | 三角形的稳定性 | B. | 四边形的不稳定性 | ||
| C. | 两点之间线段最短 | D. | 两点确定一条直线 |
| A. | $\left\{\begin{array}{l}x+y=35\\ 18x+24y=750\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=35\\ 24x+18y=750\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x-y=35\\ 24x-18y=750\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y=35\\ 18x-24y=750\end{array}\right.$ |
 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为3,∠B=135°,则$\widehat{AC}$的长( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为3,∠B=135°,则$\widehat{AC}$的长( )| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3}{2}π$ | D. | 2π |
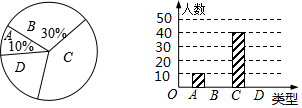 某省是劳务输出大省,农民外出务工增长家庭收入的同时,也一定程度影响了子女的管理和教育,缺少管理和教育的留守儿童的学习和心理健康状况等问题日趋显现,成为社会关注的焦点.该省相关部门就留守儿童学习和心理健康状况等问题进行调查,本次抽样调查了该省某县部分留守儿童,将调查出现的情况分四类,即A类:基本情况正常;B类;有轻度问题;C类:有较为严重问题;D类:有特别严重问题.通过调查,得到下面两幅不完整的统计图,请根据图中的信息解决下面的问题.
某省是劳务输出大省,农民外出务工增长家庭收入的同时,也一定程度影响了子女的管理和教育,缺少管理和教育的留守儿童的学习和心理健康状况等问题日趋显现,成为社会关注的焦点.该省相关部门就留守儿童学习和心理健康状况等问题进行调查,本次抽样调查了该省某县部分留守儿童,将调查出现的情况分四类,即A类:基本情况正常;B类;有轻度问题;C类:有较为严重问题;D类:有特别严重问题.通过调查,得到下面两幅不完整的统计图,请根据图中的信息解决下面的问题.