题目内容
4. 如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知:A(1,3)、A1(2,3)、A2(4,3)、A3(8,3)、B(2,0)、B1(4,0)、B2(8,0)、B3(16,0).求:
如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知:A(1,3)、A1(2,3)、A2(4,3)、A3(8,3)、B(2,0)、B1(4,0)、B2(8,0)、B3(16,0).求:(1)观察每次变换前后的三角形有何变化,找出规律.按此变换规律再将△OA3B3变换成△OA4B4,则A4的坐标是(16,3),B4的坐标是(32,0);
(2)若按第(1)题找到的规律将△OAB进行n次变换,得到△OAnBn.推测An的坐标是(2n,3),Bn的坐标是(2n+1,0);
(3)这时三角形的边变化了,跟随着三角形的形状也发生了变化,三角形横(横、纵)向放大(放大、缩小)到原来的2n倍,三角形的面积呢?
分析 (1)根据题目中的信息可以发现A1、A2、A3各点坐标的关系为横坐标是2n,纵坐标都是3,故可求得A4的坐标;B1、B2、B3各点的坐标的关系为横坐标是2n+1,纵坐标都为0,从而可求得点B4的坐标;
(2)根据(1)中发现的规律可以求得An、Bn点的坐标;
(3)根据三角形的底边后一个是前一个三角形的底边的2倍,先求出△OAnBn的底边OBn的长度,高都是4不变,然后利用三角形的面积公式分别计算出两三角形的面积,相除即可得到倍数.
解答 解:(1)∵A1(2,3)、A2(4,3)、A3(8,3).
∴A4的横坐标为:24=16,纵坐标为:3.
故点A4的坐标为:(16,3).
又∵B1(4,0)、B2(8,0)、B3(16,0).
∴B4的横坐标为:25=32,纵坐标为:0.
故点B4的坐标为:(32,0);
故答案为:(16,3),(32,0);
(2)由A1(2,3)、A2(4,3)、A3(8,3),可以发现它们各点坐标的关系为横坐标是2n,纵坐标都是3.
故An的坐标为:(2n,3).
由B1(4,0)、B2(8,0)、B3(16,0),可以发现它们各点坐标的关系为横坐标是2n+1,纵坐标都是0.
故Bn的坐标为:(2n+1,0)
故答案为:(2n,0),:(2n+1,0);
(3)根据规律,后一个三角形的底边是前一个三角形底边的2倍,高相等都是4,OBn=2n+1,
∴三角形的边变化了,跟随着三角形的形状也发生了变化,三角形横向放大到原来的2n倍,
∵S△OAnBn=$\frac{1}{2}$×2n+1×4=2n+2,
S△OAB=$\frac{1}{2}$×2×4=4,
2n+2÷4=2n,
∴△OAnBn的面积是△OAB面积的2n倍,
故答案为:边,横,放大,2n.
点评 本题考查了坐标变换的平移变换以及图形规律的探寻,发现三角形的高都是4不变,底边成2倍扩大的规律是解题的关键.

| A. | +60米 | B. | -60米 | C. | -20米 | D. | +20米 |
| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
设去年总产值x万元,总支出y万元.根据题意填写下表,并列出方程组,求x,y的值,以及今年的总产值与总支出.
| 总产值 | 总支出 | 差 | |
| 去年 | x | y | 500 |
| 今年 | x(1+15%) | y(1-10%) | 950 |
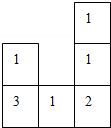 如图,是一个由若干同样大小的正方体搭成的几何体俯视图,小正方形中的数字表示在该位置的立方体的个数.
如图,是一个由若干同样大小的正方体搭成的几何体俯视图,小正方形中的数字表示在该位置的立方体的个数. 如图,已知G(4,0),点A从原点O出发,沿y轴正方向以每秒1个单位长度的速度运动,同时点D从G点出发,沿线段GO以每秒2个单位的速度运动,当点D到达O点时,A,D同时停止运动.以AD为边作正方形ABCD(字母按顺时针方向排列),设点A的运动时间为t(t>0).
如图,已知G(4,0),点A从原点O出发,沿y轴正方向以每秒1个单位长度的速度运动,同时点D从G点出发,沿线段GO以每秒2个单位的速度运动,当点D到达O点时,A,D同时停止运动.以AD为边作正方形ABCD(字母按顺时针方向排列),设点A的运动时间为t(t>0).