题目内容
13．若关于x的方程$\frac{1}{2}$mx-$\frac{5}{3}$=$\frac{1}{2}$（x-$\frac{4}{3}$）的解是正整数，则整数m为2或3．分析 先用m的代数式表示x的值，再根据方程的解是正整数解答即可．
解答 解：移项合并得：$（\frac{1}{2}m-\frac{1}{2}）x=\frac{1}{6}$，
解得：x=$\frac{2}{m-1}$，
因为方程的解是正整数，
所以m的值为2或3．
故答案为：2或3．
点评 本题主要考查了方程解的定义，关键会用m的代数式表示方程的解．
练习册系列答案
相关题目
1．
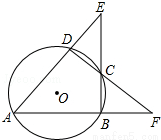如图，⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F，若∠E=α，∠F=β，则∠A等于（ ）
如图，⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F，若∠E=α，∠F=β，则∠A等于（ ）| A． | α+β | B． | $\frac{α+β}{2}$ | C． | 180°-α-β | D． | $\frac{180°-α-β}{2}$ |