题目内容
9．一个两位数，十位上数字，个位上数字分别是a、b，已知a＞b＞3，现将十位上数字，个位上数字都减去3，所在位置不变组成一个新两位数，求原两位数与新两位数之和是多少？分析 原两位数表示为10a+b，新两位数可表示为10（a-3）+b-3，然后把两个整式相加，再利用合并同类项化简即可．
解答 解：10a+b+10（a-3）+b-3
=10a+b+10a-30+b-3
=20a+2b-33．
答：原两位数与新两位数之和是20a+2b-33．
点评 本题考查了整式的加减：几个整式相加减，通常用括号把每一个整式括起来，再用加减号连接；然后去括号、合并同类项．整式的加减实质上就是合并同类项．正确表示两位数是解决本题的关键．
练习册系列答案
同步奥数系列答案
相关题目
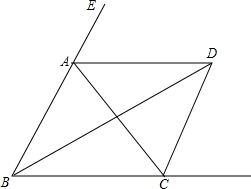如图所示，在△ABC中，AB=AC，∠EAC和∠FCA均是△ABC的外角，BD平分∠ABC，AD平分∠EAC，CD平分∠ACF，现有以下结论：①AD∥BC；②∠ADC+∠ABD=90°；③∠BDC=$\frac{1}{2}$∠BAC，其中正确的结论有①②③．