题目内容
如图，△BCD的各个顶点都在⊙A上，△BCD的角平分线BF交CD于点E，交⊙A于点F，连结CF，求证：BE2=BC•BD-EC•ED．考点：相似三角形的判定与性质,圆周角定理
专题：证明题
分析：如图，证明△BCF∽△BED，列出比例式
=
，得到BC•BD=BE•BF；由正弦定理得：BE•EF=CE•ED，两式相减即可解决问题．
| BC |
| BE |
| BF |
| BD |
解答：解：如图，∵BF平分∠CBD，
∴∠CBF=∠DBF，而∠D=∠F，
∴△BCF∽△BED，
∴
=
，BC•BD=BE•BF①；
由正弦定理得：BE•EF=CE•ED②，
由①-②得：BE（BF-EF）=BC•BD-CE•ED，
即BE2=BC•BD-EC•ED．
解：如图，∵BF平分∠CBD，∴∠CBF=∠DBF，而∠D=∠F，
∴△BCF∽△BED，
∴
| BC |
| BE |
| BF |
| BD |
由正弦定理得：BE•EF=CE•ED②，
由①-②得：BE（BF-EF）=BC•BD-CE•ED，
即BE2=BC•BD-EC•ED．
点评：该题以圆为载体，以圆周角定理及其推论、相似三角形的判定及其性质为考查的核心构造而成；牢固掌握圆周角定理及其推论、相似三角形的判定及其性质是解题的关键．
练习册系列答案
相关题目
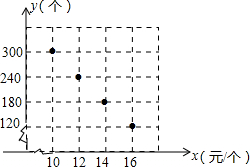某校部分团员参加社会公益活动，准备购进一批许愿瓶进行销售，并将所得利润捐给慈善机构．这种许愿瓶的进价为6元/个，根据市场调查，一段时间内的销售量y（个）与销售单价x（元/个）之间的对应关系如图所示：
求阴影部分的面积．（取π=3）
如图所示，已知DE∥BC，AE=50cm，EC=30cm，BC=70cm，∠A=45°，∠C=40°，求：
如图，已知线段AC，点D为AC的中点，BC=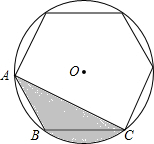
如图，在半径为6cm的圆内画一个正六边形，求阴影部分的面积．
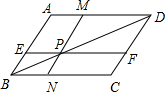如图，?ABCD中，EF∥AD，MN∥AB，MN与EF交于点P，且点P在BD上．