题目内容
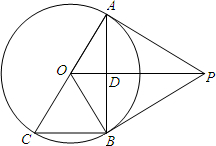 如图,PA、PB是⊙O的切线,A、B是切点,AC是⊙O的直径,AB交OP于D.
如图,PA、PB是⊙O的切线,A、B是切点,AC是⊙O的直径,AB交OP于D.(1)证明:AD⊥OP;
(2)若AC=10,sinC=
| 3 |
| 5 |
考点:切线的性质
专题:计算题
分析:(1)由PA与PB为圆O的切线,利用切线长定理得到PO为角平分线,利用三线合一即可得证;
(2)由AC为圆O的直径,利用直径所对的圆周角为直角得到AB垂直于BC,再由OP垂直于AB,得到OP与BC平行,利用两直线平行同位角相等得到∠AOP=∠C,进而得到sinC=sin∠AOP,由AC求出OA的长,在直角三角形AOP中,设OA=3x,得到OP=5x,AP=4x,求出x的值,即可确定出PA的长.
(2)由AC为圆O的直径,利用直径所对的圆周角为直角得到AB垂直于BC,再由OP垂直于AB,得到OP与BC平行,利用两直线平行同位角相等得到∠AOP=∠C,进而得到sinC=sin∠AOP,由AC求出OA的长,在直角三角形AOP中,设OA=3x,得到OP=5x,AP=4x,求出x的值,即可确定出PA的长.
解答:(1)证明:∵PA、PB为圆O的切线,
∴PO平分∠APB,PA=PB,
∴AD⊥OP;
(2)解:∵AC为直径,
∴AB⊥BC,
∵OP⊥BC,
∴OP∥BC,
∴∠AOP=∠C,
∴sin∠AOP=sinC=
,
∵PA为圆O的切线,
∴OA⊥PA,
在Rt△AOP中,设OA=5=3x,则OP=5x,
则PA=4x=
.
∴PO平分∠APB,PA=PB,
∴AD⊥OP;
(2)解:∵AC为直径,
∴AB⊥BC,
∵OP⊥BC,
∴OP∥BC,
∴∠AOP=∠C,
∴sin∠AOP=sinC=
| 3 |
| 5 |
∵PA为圆O的切线,
∴OA⊥PA,
在Rt△AOP中,设OA=5=3x,则OP=5x,
则PA=4x=
| 25 |
| 3 |
点评:此题考查了切线的性质,切线长定理,等腰三角形的性质,以及锐角三角函数定义,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
下列计算不正确的是.( )
| A、(x-1)(-1-x)=1-x2 |
| B、(x+1)2=x2+1 |
| C、(-x)3÷(-x)2=-x |
| D、(-3a5)2÷(a2)3=9a4 |
在0,-3,1,2这四个数中,最小的数是( )
| A、0 | B、-3 | C、1 | D、2 |
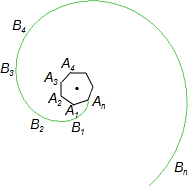 如图,正多边形A1、A2、A3、A4…An,曲线B1B2B3B4…Bn叫做“正多边形的渐开线”,其中AnB1、B1B2、B2B3、B3B4…的圆心依次按A1、A2、A3、A4…循环.循环一周就叫一周曲线长,当A1A2=1时,一周曲线长为
如图,正多边形A1、A2、A3、A4…An,曲线B1B2B3B4…Bn叫做“正多边形的渐开线”,其中AnB1、B1B2、B2B3、B3B4…的圆心依次按A1、A2、A3、A4…循环.循环一周就叫一周曲线长,当A1A2=1时,一周曲线长为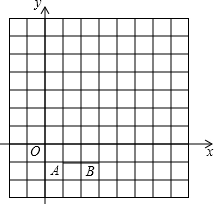 已知线段AB平行于x轴且点A在点B的左侧,AB=2,点A的坐标为(1,-1),将线段AB先向上平移3个单位,再向左平移1个单位后的线段为CD,点A与点C对应,则点D的坐标为
已知线段AB平行于x轴且点A在点B的左侧,AB=2,点A的坐标为(1,-1),将线段AB先向上平移3个单位,再向左平移1个单位后的线段为CD,点A与点C对应,则点D的坐标为