题目内容
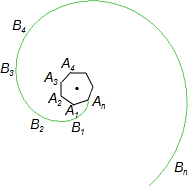 如图,正多边形A1、A2、A3、A4…An,曲线B1B2B3B4…Bn叫做“正多边形的渐开线”,其中AnB1、B1B2、B2B3、B3B4…的圆心依次按A1、A2、A3、A4…循环.循环一周就叫一周曲线长,当A1A2=1时,一周曲线长为
如图,正多边形A1、A2、A3、A4…An,曲线B1B2B3B4…Bn叫做“正多边形的渐开线”,其中AnB1、B1B2、B2B3、B3B4…的圆心依次按A1、A2、A3、A4…循环.循环一周就叫一周曲线长,当A1A2=1时,一周曲线长为考点:弧长的计算
专题:压轴题,规律型
分析:观察图中可以发现曲线EFGHIJ的长度是由n个从小到大的扇形弧长组成的,所以利用弧长公式即可求出.
解答: 解:正多边形A1A2A3A4…An,的每个外角都等于
解:正多边形A1A2A3A4…An,的每个外角都等于
,
∵AnB1、B1B2、B2B3、B3B4…的圆心依次按A1、A2、A3、A4…循环,当A1A2=1时,
∴半径依次为1、2、3、…,n,
∴一周曲线长=
+
+
+…+
=
(1+2+3+…+n)π=
•
π=(n+1)π.
故答案为(n+1)π.
 解:正多边形A1A2A3A4…An,的每个外角都等于
解:正多边形A1A2A3A4…An,的每个外角都等于| 360° |
| n |
∵AnB1、B1B2、B2B3、B3B4…的圆心依次按A1、A2、A3、A4…循环,当A1A2=1时,
∴半径依次为1、2、3、…,n,
∴一周曲线长=
| ||
| 180 |
| ||
| 180 |
| ||
| 180 |
| ||
| 180 |
| 2 |
| n |
| 2 |
| n |
| n(n+1) |
| 2 |
故答案为(n+1)π.
点评:本题考查了弧长的计算:弧长=
(n为弧所对的圆心角的度数,R为圆的半径).也考查了正多边形的性质.
| n•π•R |
| 180 |

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
由五个完全相同的小正方形组合而成的立体图形如图所示,它的正视图是( )

A、 |
B、 |
C、 |
D、 |

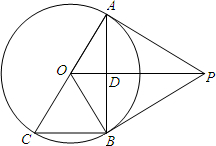 如图,PA、PB是⊙O的切线,A、B是切点,AC是⊙O的直径,AB交OP于D.
如图,PA、PB是⊙O的切线,A、B是切点,AC是⊙O的直径,AB交OP于D.



