题目内容
6.先化简,再求值:(x-2-$\frac{5}{x+2}$)÷$\frac{x-3}{2x+4}$,其中x=$\sqrt{2}$+3.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{(x+2)(x-2)-5}{x+2}$÷$\frac{x-3}{2(x+2)}$=$\frac{(x+3)(x-3)}{x+2}$•$\frac{2(x+2)}{x-3}$=2(x+3),
当x=$\sqrt{2}$+3时,原式=2($\sqrt{2}$+6)=2$\sqrt{2}$+12.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
17.[x]表示不超过实数x的最大整数(如[π]=3,[-π]=-4,[-4]=-4),记M=[x]+[2x]+[3x],将不能表示成M形式的正整数称为“隐形数”,则不超过2014的“隐形数”的个数是( )
| A. | 335 | B. | 336 | C. | 670 | D. | 671 |
14.2010年3月温家宝总理在2010年政府工作报告中指出和2009在国际金融危机的冲击下,我国国内生产总值仍高达33.5万亿元,比上年增长8.7%,33.5万亿用科学记数法表示为( )
| A. | 33.5×109 | B. | 33.5×1012 | C. | 33.5×1012 | D. | 3.35×1013 |
11.关于x的方程x-2=m的解为正实数,则m的取值范围是( )
| A. | m≥2 | B. | m≤2 | C. | m>-2 | D. | m<2 |
18.下列方程的解是x=2的方程是( )
| A. | 4x+8=0 | B. | -$\frac{1}{3}$x+$\frac{2}{3}$=0 | C. | $\frac{2}{3}$x=2 | D. | 1-3x=5 |
15.在五边形ABCDE中,已知∠A与∠C互补,∠B+∠D=270°,则∠E的度数为( )
| A. | 80° | B. | 90° | C. | 100° | D. | 110° |
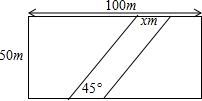 如图,在草坪中间修一条小路,小路的横向宽为x m,设开辟道路后草地的实际面积为y m2.
如图,在草坪中间修一条小路,小路的横向宽为x m,设开辟道路后草地的实际面积为y m2.