题目内容
一个多边形,它的内角和比外角和的3倍少180°,求这个多边形的边数、内角和度数及对角线的条数.
考点:多边形内角与外角
专题:
分析:多边形的内角和比外角和的3倍少180°,而多边形的外角和是360°.n边形的内角和可以表示成(n-2)•180°,设这个多边形的边数是n,就得到方程,从而求出边数.
解答:解:根据题意,得
(n-2)•180=360°×3-180,
解得:n=7.
则这个多边形的边数是7,内角和度数是5×180°=900°,
对角线为
=14条.
(n-2)•180=360°×3-180,
解得:n=7.
则这个多边形的边数是7,内角和度数是5×180°=900°,
对角线为
| 7(7-3) |
| 2 |
点评:考查了多边形内角与外角.此题比较简单,只要结合多边形的内角和公式寻求等量关系,构建方程即可求解.

练习册系列答案
相关题目
若α,β是一元二次方程x2-3x+1=0的两根,则α2+β2的值是( )
| A、6 | B、7 | C、8 | D、9 |
下列说法不正确的是( )
| A、两个单项式的积仍是单项式 |
| B、两个单项式的积的次数等于它们的次数之和 |
| C、单项式乘以多项式,积的项数与多项式项数相同 |
| D、多项式乘以多项式,合并同类项前,积的项数等于两个多项式的项数之和 |
 如图,AC是⊙O的弦,以OA为直径的圆交AC于点E.
如图,AC是⊙O的弦,以OA为直径的圆交AC于点E.
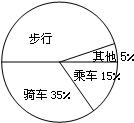 某校对全校2560名学生的上学方式进行了一次抽样调查,右图是根据此次调查结果所绘制的一个未完成的扇形统计图,被调查的学生中骑车的有21人,则下列四种说法:
某校对全校2560名学生的上学方式进行了一次抽样调查,右图是根据此次调查结果所绘制的一个未完成的扇形统计图,被调查的学生中骑车的有21人,则下列四种说法: △ABC中,∠A=60°,∠ABC和∠ACB的平分线相交于点P,则∠BPC=
△ABC中,∠A=60°,∠ABC和∠ACB的平分线相交于点P,则∠BPC=