题目内容
已知四个连续非0自然数的倒数之和等于
，求这四个自然数．
| 19 |
| 20 |
考点：整数问题的综合运用
专题：
分析：设出四个连续非0自然数分别为a，a+1，a+2，a+3，表示出其倒数，根据题意列出等式，推知a的值，即可得到四个自然数．
解答：解：设所求四个连续非0自然数分别为a，a+1，a+2，a+3，
则
+
+
+
=
，
＞
，
解得a＜4
，
当a=1时，
+
+
+
=1+
+
+
=
，不合题设条件；
当a=2时，
+
+
+
=
+
+
+
=
，不合题设条件；
当a=3时，
+
+
+
=
+
+
+
=
，符合题设条件；
当a=4时，
+
+
+
=
+
+
+
=
，不合题设条件．
所以这四个自然数为3，4，5，6．
则
| 1 |
| a |
| 1 |
| a+1 |
| 1 |
| a+2 |
| 1 |
| a+3 |
| 19 |
| 20 |
| 1 |
| a |
| 19 |
| 20×4 |
解得a＜4
| 4 |
| 19 |
当a=1时，
| 1 |
| a |
| 1 |
| a+1 |
| 1 |
| a+2 |
| 1 |
| a+3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 25 |
| 12 |
当a=2时，
| 1 |
| a |
| 1 |
| a+1 |
| 1 |
| a+2 |
| 1 |
| a+3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 77 |
| 60 |
当a=3时，
| 1 |
| a |
| 1 |
| a+1 |
| 1 |
| a+2 |
| 1 |
| a+3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 19 |
| 20 |
当a=4时，
| 1 |
| a |
| 1 |
| a+1 |
| 1 |
| a+2 |
| 1 |
| a+3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 7 |
| 319 |
| 420 |
所以这四个自然数为3，4，5，6．
点评：此题考查了整数问题的综合运用，设出四个数，根据题意推理出相关数值是解题的关键，要注意相关值的取舍，需进行验算．
练习册系列答案
相关题目
一个长方形的长减少5cm，宽增加2cm，就成为一个正方形，并且这两个图形的面积相等，若设这个长方形的长为xcm，宽为ycm，则可列方程组（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
如图，在我们横店的某旅游景点，为了增加旅游的乐趣，特安排了一次寻宝游戏，寻宝人已经找到了坐标为A（1，-3）和B（1，3）的两个标志点，并且知道藏宝地点的坐标为（3，2），除此外不知其他信息，如何确定坐标系找”宝藏”？请互相合作交流．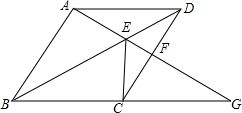
四边形ABCD是边长为2的菱形，点G是BC延长线上一点，连接AG，AG⊥AB，分别交DB、CD于点E、F，连接CE．若AE=2EF，求EF长．
细心观察图形，认真分析各式，然后解答问题．
画图：牧童在A处放牛，其家在B处，若牧童从A处将牛牵到河边C处饮水后再回家，试问C在何处，所走路程最短？（保留作图痕迹）