题目内容
15.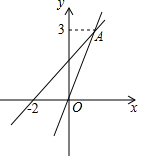 已知正比例函数y=mx与一次函数y=ax+b的图象交于点A(1,3);
已知正比例函数y=mx与一次函数y=ax+b的图象交于点A(1,3);(1)求这两个函数的解析式;
(2)求该一次函数的图象与坐标轴所围成的三角形的面积;
(3)根据图象回答x取何值时,正比例函数的值大于一次函数的值.
分析 (1)把A(1,3)代入y=mx,利用待定系数法求得正比例函数的解析式;把A(1,3),(-2,0)代入y=ax+b,再利用待定系数法求得一次函数的解析式;
(2)首先求得一次函数与y轴的交点坐标,再根据三角形的面积公式列式计算即可求得答案;
(3)观察图象,即可求得正比例函数的值大于一次函数的值时x的取值范围.
解答 解:(1)把A(1,3)代入y=mx,得m=3,
则正比例函数的解析式为y=3x;
把A(1,3),(-2,0)代入y=ax+b,
得$\left\{\begin{array}{l}{a+b=3}\\{-2a+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$,
则一次函数的解析式为:y=x+2;
(2)∵一次函数的解析式为:y=x+2,
∴一次函数与y轴的交点坐标为:(0,2),
又一次函数与x轴的交点坐标为:(-2,0),
∴该一次函数的图象与坐标轴所围成的三角形的面积为:$\frac{1}{2}$×2×2=2;
(3)正比例函数的值大于一次函数的值时x的取值范围为:x>1.
点评 此题考查了两条直线的交点问题,待定系数法求一次函数的解析式,三角形的面积.正确求出两个函数的解析式是解此题的关键.

练习册系列答案
相关题目
5.一种登革热病毒的直径约为0.00000005m,数据0.00000005m可用科学记数法表示为( )
| A. | 5×10-7m | B. | 5×10-8m | C. | 0.5×10-7m | D. | -5×108m |
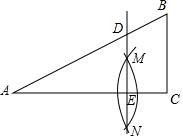 如图,在△ABC中,∠ACB=90°,以点A为圆心,以某一长度为半径画弧,再以点C为圆心,以另一长度为半径画弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E.求证:DE∥BC.
如图,在△ABC中,∠ACB=90°,以点A为圆心,以某一长度为半径画弧,再以点C为圆心,以另一长度为半径画弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E.求证:DE∥BC.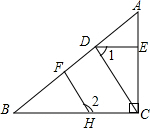 如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补.求证:HF⊥AB.
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补.求证:HF⊥AB.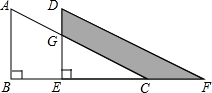 如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF,其中AB=8,DG=3,BE=6,求图中阴影部分的面积.
如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF,其中AB=8,DG=3,BE=6,求图中阴影部分的面积. 如图.已知△ABC中,△ADE∽△ABC,AD:BD=3:4,求S△ADE:S四边形DECB.
如图.已知△ABC中,△ADE∽△ABC,AD:BD=3:4,求S△ADE:S四边形DECB.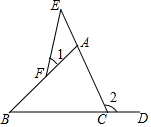 如图所示,∠1,∠2是不是△ABC的外角?图中还有哪些角可以看作一个三角形的外角?
如图所示,∠1,∠2是不是△ABC的外角?图中还有哪些角可以看作一个三角形的外角?
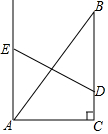 如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=4,点D在BC上,以AB为对角线的所有平行四边形ADBE中,DE的最小值是3.
如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=4,点D在BC上,以AB为对角线的所有平行四边形ADBE中,DE的最小值是3.