题目内容
14.汽车油箱中的余油量Q(升)与它行驶的时间t(小时)之间的关系如下表:| 余油量Q/L | 60 | 50 | 40 | 30 | 20 | … |
| 行驶时间t/h | 0 | 2 | 4 | 6 | 8 | … |
(2)从开始算起,如果汽车每小时行驶40千米,当油箱中的油耗尽时,该汽车行驶了多少千米?
分析 (1)利用待定系数法求出一次函数解析式得出即可;
(2)利用(1)中所求得出汽车行驶的时间,进而求出行驶的总路程.
解答 解:(1)设油箱中的余油量Q与行驶时间t的函数关系式为:Q=kt+b,
则$\left\{\begin{array}{l}{2k+b=50}\\{4k+b=40}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-5}\\{b=60}\end{array}\right.$.
故油箱中的余油量Q与行驶时间t的函数关系式为:Q=-5t+60;
(2)由题意可得:当Q=0时,0=-5t+60,
解得:t=12,
则S=12×40=480(km).
答:该汽车行驶了480千米.
点评 此题主要考查了函数关系式以及函数值,利用待定系数法求出一次函数解析式是解题关键.

练习册系列答案
相关题目
3.下列由2和3组成的四个算式中,值最小的是( )
| A. | 2-3 | B. | 2÷3 | C. | 23 | D. | 2-3 |
4.下列各数中,是有理数的是( )
| A. | $\root{3}{2}$ | B. | $-\sqrt{3}$ | C. | π | D. | $\frac{1}{3}$ |
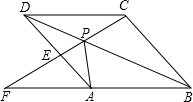 如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.试问:
如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.试问: