题目内容
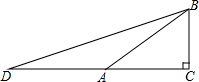已知：如图，Rt△ABC中，∠C=90°，∠BAC=30°，延长CA至D点，使AD=AB．（1）求∠D及∠DBC的度数；
（2）求tanD及tan∠DBC；
（3）用类似方法，求tan22.5°．
考点：解直角三角形
专题：计算题
分析：（1）由AB=AD得到∠D=∠ABD，而∠BAC=∠D+∠ABD=30°，所以∠D=15°，然后利用互余得到∠DBC=75°；
（2）设BC=x，在Rt△ABC中根据含30度的直角三角形三边的关系得到AB=2BC=2x，AC=
BC=
x，则AD=AB=2x，DC=AD+AC=（2+
）x，然后根据正切易得tanD=2-
，tan∠DBC=2+
；
（3）如图，在Rt△ABC中，∠BAC=45°，延长CA至D点，使AD=AB，则∠D=22.5°，设BC=a，在△ABC等腰直角三角形中，AC=a，AB=
a，则AD=
a，
所以CD=DA+AC=（
+1）a，在Rt△BCD中，根据正切的定义易得tanD=
-1，即tan22.5=
-1．
（2）设BC=x，在Rt△ABC中根据含30度的直角三角形三边的关系得到AB=2BC=2x，AC=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
（3）如图，在Rt△ABC中，∠BAC=45°，延长CA至D点，使AD=AB，则∠D=22.5°，设BC=a，在△ABC等腰直角三角形中，AC=a，AB=
| 2 |
| 2 |
所以CD=DA+AC=（
| 2 |
| 2 |
| 2 |
解答：解：（1）∵AB=AD，
∴∠D=∠ABD，
∵∠BAC=∠D+∠ABD=30°，
∴∠D=15°；
∴∠DBC=90°-∠D=75°；
（2）设BC=x，
在Rt△ABC中，∵∠BAC=30°，
∴AB=2BC=2x，AC=
BC=
x，
∴AD=AB=2x，
∴DC=AD+AC=（2+
）x，
在Rt△BCD中，
tanD=
=
=2-
，
tan∠DBC=
=
=2+
；
（3）如图，在Rt△ABC中，∠BAC=45°，延长CA至D点，使AD=AB，
则∠D=22.5°，
设BC=a，
∵△ABC等腰直角三角形，
∴AC=a，AB=
a，
∴AD=
a，
∴CD=DA+AC=（
+1）a，
在Rt△BCD中，tanD=
=
=
-1，
即tan22.5=
-1．
∴∠D=∠ABD，
∵∠BAC=∠D+∠ABD=30°，
∴∠D=15°；
∴∠DBC=90°-∠D=75°；
（2）设BC=x，
在Rt△ABC中，∵∠BAC=30°，
∴AB=2BC=2x，AC=
| 3 |
| 3 |
∴AD=AB=2x，
∴DC=AD+AC=（2+
| 3 |
在Rt△BCD中，
tanD=
| BC |
| DC |
| x | ||
(2+
|
| 3 |
tan∠DBC=
| DC |
| BC |
(2+
| ||
| x |
| 3 |
（3）如图，在Rt△ABC中，∠BAC=45°，延长CA至D点，使AD=AB，
则∠D=22.5°，
设BC=a，
∵△ABC等腰直角三角形，
∴AC=a，AB=
| 2 |
∴AD=
| 2 |
∴CD=DA+AC=（
| 2 |
在Rt△BCD中，tanD=
| BC |
| DC |
| x | ||
(
|
| 2 |
即tan22.5=
| 2 |
点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
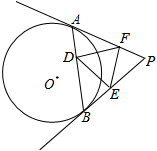如图，PA、PB切⊙O于点A、B，连结AB，在AB、PA、PB上分别取点D、F、E，使AD=BE，BD=AF，连结DE、DF、EF，若∠P=α，求∠EDF（用含α的代数式表示）