题目内容
4.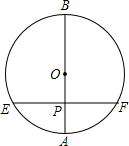 如图所示,在⊙O中,直径AB⊥弦EF,垂足为P,AP=1cm,BP=3cm,EF等于( )
如图所示,在⊙O中,直径AB⊥弦EF,垂足为P,AP=1cm,BP=3cm,EF等于( )| A. | 2$\sqrt{3}$cm | B. | $\sqrt{3}$cm | C. | 2cm | D. | 4cm |
分析 连接OF,先根据AP=1cm,BP=3cm得出AB的长,故可得出OP及OF的长,由勾股定理求出PF的长,进而可得出结论.
解答 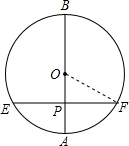 解:连接OF,
解:连接OF,
∵AP=1cm,BP=3cm,
∴AB=1+3=4cm,
∴OF=2cm,OP=1cm.
∵AB⊥CD,
∴PF=$\sqrt{{OF}^{2}-{OP}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∵AB是⊙O的直径,
∴EF=2PF=2$\sqrt{3}$cm.
故选A.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.下列计算错误的是( )
| A. | (23)2×24=210 | B. | (-c)3(-c)5=c8 | C. | 32×(-3)4=(-3)6 | D. | 5×(-$\frac{1}{2}$)2=20 |
 如图,△ABC中,$\frac{DC}{DB}$=$\frac{EA}{EC}$=$\frac{FB}{FA}$=$\frac{1}{2}$,求$\frac{△GHI的面积}{△ABC的面积}$的值.
如图,△ABC中,$\frac{DC}{DB}$=$\frac{EA}{EC}$=$\frac{FB}{FA}$=$\frac{1}{2}$,求$\frac{△GHI的面积}{△ABC的面积}$的值.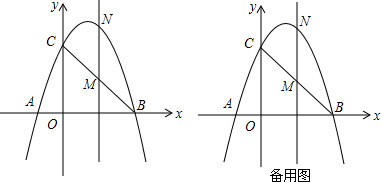
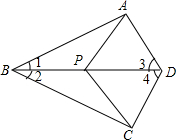 如图,在四边形ABCD中,点P是对角线BD上任意一点,∠1=∠2,∠3=∠4.求证:PA=PC.
如图,在四边形ABCD中,点P是对角线BD上任意一点,∠1=∠2,∠3=∠4.求证:PA=PC.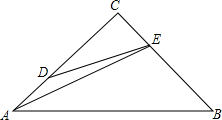 如图,已知△ABC,∠ACB=90°,AC=BC,点D在AC上,点E在BC上,AD=CE,CD=2AD,求证:∠CDE=∠EAB.
如图,已知△ABC,∠ACB=90°,AC=BC,点D在AC上,点E在BC上,AD=CE,CD=2AD,求证:∠CDE=∠EAB.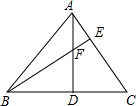 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分为D、E,AD=BD=2,则AF+DC=2.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分为D、E,AD=BD=2,则AF+DC=2.