题目内容
13.计算:(1)8x2y4•(-$\frac{3x}{4{y}^{3}}$)÷(-$\frac{{x}^{2}y}{2}$)
(2)$\frac{2x-6}{x-2}÷$($\frac{5}{x-2}-x-2$)
分析 (1)首先把乘除统一成乘法计算,然后进行约分即可;
(2)首先对括号内的分式进行通分相加,然后把除法转化为乘法,进行乘法计算即可.
解答 解:(1)原式=8x2y4•$\frac{3x}{4{y}^{3}}$•$\frac{2}{{x}^{2}y}$=12x;
(2)原式=$\frac{2(x-3)}{x-2}$÷$\frac{5-(x-2)(x+2)}{x-2}$=$\frac{2(x-3)}{x-2}$÷$\frac{(x+3)(3-x)}{x-2}$=$\frac{2(x-3)}{x-2}$•$\frac{x-2}{(x+3)(3-x)}$=-$\frac{2}{x+3}$.
点评 本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.

练习册系列答案
相关题目
4.若a>b,则下列式子正确的是( )
| A. | a-4>b-3 | B. | $\frac{1}{2}$a<$\frac{1}{2}$b | C. | -3a>-3b | D. | 3+2a>3+2b |
8.已知4x2-kxy+y2是完全平方式,则常数k等于( )
| A. | 4 | B. | -4 | C. | ±4 | D. | 2 |
18.抛物线y=x2-2x+2的顶点坐标为( )
| A. | (1,1) | B. | (1,2) | C. | (-1,1) | D. | (-1,2) |

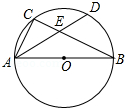 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为$\frac{14}{5}$.
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为$\frac{14}{5}$.