题目内容
5．
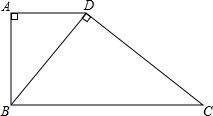已知，如图，梯形ABCD中，AD∥BC，∠A=90°，BC=10，CD=8，对角线BD⊥CD．（1）求证：△ABD∽△DCB；
（2）求AD的长．
分析 （1）由AD∥BC可知∠ADB=∠DBC，又∠A=∠BDC=90°，故△ABD和△DC相似；
（2）首先根据勾股定理求出BD=6，然后根据△ABD∽△DCB，列比例式求解即可．
解答 （1）证明：∵AD∥BC，
∴∠ADB=∠DBC，
∵∠A=∠BDC=90°，
∴△ABD∽△DCB，
（2）解：在直角三角形BDC中，
BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=6，
∵△ABD∽△DCB，
∴AD：BD=BD：BC，
即AD：6=6：10，
∴AD=3.6．
点评 本题主要考查了相似三角形的判定与性质以及勾股定理，熟悉相似三角形的判定方法是解决问题的关键．
练习册系列答案
相关题目
4．把点（2，-3）先向左平移3个单位长度，再向下平移2个单位长度得到的点的坐标是（ ）
| A． | （-1，-5） | B． | （5，-1） | C． | （5，-5） | D． | （-1，-1） |
5．下列计算正确的是（ ）
| A． | a•a3=a3 | B． | a4+a3=a2 | C． | （a2）5=a7 | D． | （-ab）2=a2b2 |
2．某校学生小明每天骑自行车上学时都要经过一个十字路口，设十字路口有红、黄、绿三色交通信号灯，他在路口遇到红灯的概率为$\frac{1}{3}$，遇到黄灯的概率为$\frac{1}{9}$，那么他遇到绿灯的概率为（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{2}{9}$ | C． | $\frac{4}{9}$ | D． | $\frac{5}{9}$ |
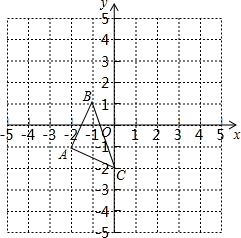如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-2，-1）、B（-1，1）、C（0，-2）．
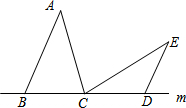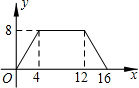
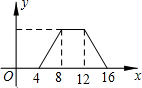
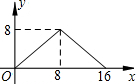
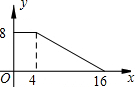
如图：在△ABC和△CDE中，AB=AC=CE，BC=DC=DE，AB＞BC，∠BAC=∠DCE，点B，C，D在直线m上．以点C为旋转中心，将△CDE按逆时针方向旋转，使得CE与CA重合，得到△CD1E1（A）．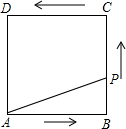
如图，正方形ABCD的边长为4，P为正方形边上一动点，运动路线是A→B→C→D→A，设P点经过的路程为x，以点A，P，B为顶点的三角形的面积是y，则下列图象能大致描述y与x的函数关系的是（ ）
