题目内容
6.在△ABC中,BE平分△ABC交AC于点E,ED∥CB交AB于点D,若AD=2,DE=3,AE=4,求AC的长.分析 因为ED∥CB,所以∠1=∠3,又因为BE平分∠ABC,所以∠1=∠2.故∠2=∠3,根据等角对等边,BD=DE=2,根据平行线分线段成比例定理,$\frac{AD}{AB}=\frac{AE}{AC}$,于是得到结论.
解答 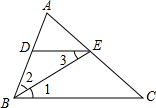 解:∵ED∥CB,
解:∵ED∥CB,
∴∠1=∠3,
又∵BE平分∠ABC,
∴∠1=∠2,
∴∠2=∠3,
∴BD=DE=3,
又∵ED∥CB,
∴$\frac{AD}{AB}=\frac{AE}{AC}$,
∵AD=2,DE=3,
∴AB=AD+BD=AD+DE=5,
即$\frac{2}{5}$=$\frac{4}{AC}$,
∴AC=10.
点评 此题考查了平行线的性质和平行线分线段成比例定理,构思巧妙,是一道很好的题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
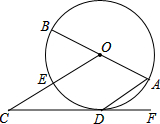 如图,AB是⊙O的直径,点D是⊙O上的一点,OC∥AD交⊙O于点E,点F在CD的延长线上,∠BOC+∠ADF=90°.
如图,AB是⊙O的直径,点D是⊙O上的一点,OC∥AD交⊙O于点E,点F在CD的延长线上,∠BOC+∠ADF=90°.
 某花卉市场举行开业庆祝活动,组织者按树木花草的品种和大小,摆成如图所示的图案(每个小圆点代表一盆花),试求第n个图形需要多少盆花?
某花卉市场举行开业庆祝活动,组织者按树木花草的品种和大小,摆成如图所示的图案(每个小圆点代表一盆花),试求第n个图形需要多少盆花?