Question

16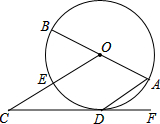．如图，AB是⊙O的直径，点D是⊙O上的一点，OC∥AD交⊙O于点E，点F在CD的延长线上，∠BOC+∠ADF=90°．
（1）求证：CD是⊙O的切线；
（2）若AB=6，CD=4，求CE．

Answer 1

分析 （1）连结OD，由OC∥AD得到∠BOC=∠A，而∠ODA=∠A，则∠ODA=∠BOC，由于∠BOC+∠ADF=90°，所以∠ODA+∠ADF=90°，然后根据切线的判定定理得到结论；
（2）延长CO交⊙O于H，于是得到EH=AB=6，根据切割线定理即可得到结论．

解答 （1）证明：连结OD，如图，
∵OC∥AD，
∴∠BOC=∠A，
而OD=OA，
∴∠ODA=∠A，
∴∠ODA=∠BOC，
∵∠BOC+∠ADF=90°，
∴∠ODA+∠ADF=90°，
即∠ODF=90°，
∴OD⊥DF，
∴CD是⊙O的切线；

（2）延长CO交⊙O于H，
∴EH=AB=6，
∵CD是⊙O的切线，
∴CD²=CE•CH，
即4²=CE（CE+6），
∴CE=2（负值舍去）．

点评 本题考查了切线的判定定理，切割线定理，知道经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键．