题目内容
6.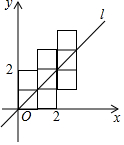 如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为y=$\frac{10}{9}$x-$\frac{10}{3}$.
如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为y=$\frac{10}{9}$x-$\frac{10}{3}$.
分析 设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥y轴于C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标即可得到该直线l的解析式.
解答 解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥y轴于C
∵正方形的边长为1,
∴OB=3,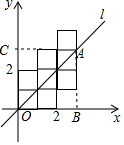
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴两边分别是4,
∴三角形ABO面积是5,
∴$\frac{1}{2}$OB•AB=5,
∴AB=$\frac{10}{3}$,
∴OC=$\frac{10}{3}$,
由此可知直线l经过(3,$\frac{10}{3}$),
设直线方程为y=kx,
则$\frac{10}{3}$=3k,
k=$\frac{10}{9}$,
∴直线l解析式为y=$\frac{10}{9}$x,
∴将直线l向右平移3个单位后所得直线l′的函数关系式为y=$\frac{10}{9}$x-$\frac{10}{3}$;
故答案为:y=$\frac{10}{9}$x-$\frac{10}{3}$.
点评 此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质,此题难度较大,解题的关键是作AB⊥y轴,作AC⊥x轴,根据题意即得到:直角三角形ABO,利用三角形的面积公式求出AB的长.

练习册系列答案
相关题目
16. 如图,在矩形ABCD中,AB=3,∠AOB=60°,则OC的长为( )
如图,在矩形ABCD中,AB=3,∠AOB=60°,则OC的长为( )
 如图,在矩形ABCD中,AB=3,∠AOB=60°,则OC的长为( )
如图,在矩形ABCD中,AB=3,∠AOB=60°,则OC的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.2014年元月的某一天,我县的最低气温为-1℃,最高气温为4℃,那么这天的日温差是( )
| A. | 3℃ | B. | 4℃ | C. | -5℃ | D. | 5℃ |
 如图,AB为⊙O的直径,D为$\widehat{AC}$的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.
如图,AB为⊙O的直径,D为$\widehat{AC}$的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.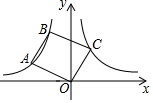 如图,点A、B在双曲线y=$\frac{3}{x}$(x<0)上,连接OA、AB,以OA、AB为边作?OABC.若点C恰落在双曲线y=$\frac{2}{x}$(x>0)上,此时?OABC的面积为2$\sqrt{7}$.
如图,点A、B在双曲线y=$\frac{3}{x}$(x<0)上,连接OA、AB,以OA、AB为边作?OABC.若点C恰落在双曲线y=$\frac{2}{x}$(x>0)上,此时?OABC的面积为2$\sqrt{7}$.