题目内容
20.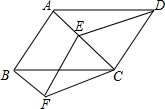 已知:如图,在四边形ABCD中,AB∥CD,点E是对角线AC上一点,∠ADC=∠ABC.
已知:如图,在四边形ABCD中,AB∥CD,点E是对角线AC上一点,∠ADC=∠ABC.(1)求证:四边形ABCD是平行四边形;
(2)分别过点E、B作AB和AC的平行线交于点F,连接CF,若∠FCE=∠DCE,求证:四边形EFCD是菱形.
分析 (1)欲证明四边形ABCD是平行四边形,只需推知AD∥BC;
(2)根据平行四边形的定义求出四边形ABFE是平行四边形,根据平行四边形对边平行且相等可得AB∥EF,AB=EF,再求出CD∥EF,CD=EF,然后利用一组对边平行且相等的四边形是平行四边形求出四边形EFCD是平行四边形,根据两直线平行,内错角相等可得∠FEC=∠ECD,从而求出∠FEC=∠FCE,根据等边对等角可得EF=FC,再根据邻边相等的平行四边形是菱形求出平行四边形EFCD是菱形.
解答 证明:(1)∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵∠ADC=∠ABC,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
又AB∥CD,
∴四边形ABCD是平行四边形;
(2)∵EF∥AB,BF∥AE,
∴四边形ABFE是平行四边形,
∴AB∥EF,AB=EF,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴CD∥EF,CD=EF,
∴四边形EFCD是平行四边形,
∵CD∥EF,
∴∠FEC=∠ECD,
又∵∠DCE=∠FCE,
∴∠FEC=∠FCE,
∴EF=FC,
∴平行四边形EFCD是菱形.
点评 本题考查平行四边形、菱形的判定,具体选择哪种方法需要根据已知条件来确定.

练习册系列答案
相关题目
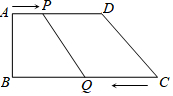 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24厘米,AB=8厘米,BC=30厘米,动点P从A开始沿AD边向D以每秒1厘米的速度运动,动点Q从点C开始沿CB边向B以每秒3厘米的速度运动,P,Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t秒.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24厘米,AB=8厘米,BC=30厘米,动点P从A开始沿AD边向D以每秒1厘米的速度运动,动点Q从点C开始沿CB边向B以每秒3厘米的速度运动,P,Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t秒.