Question

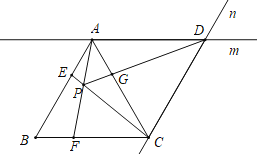
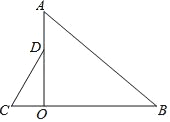
【题目】如图，在△ABC中，∠BAC＝90°，AB＝3，AC＝4，△ADE的顶点D在BC上运动，且∠DAE＝90°，∠ADE＝∠B，F为线段DE的中点，连接CF，在点D运动过程中，线段CF长的最小值为_____．

Answer 1

【答案】2

【解析】

连接CE，利用相似进行转化先得出∠DCE=90°，F是DE的中点，可得CF=DE，再根据当AD⊥BC时，AD最短，此时DE最短，根据直角三角形的面积以及相似三角形的性质，求得DE的最小值，即可得出CF的最小值．

解：连接CE，如图所示：

BC＝＝＝5，

∵∠BAC＝∠DAE＝90°，∠ADE＝∠B，

∴△ABC∽△ADE，

∴＝，∠ACD＝∠AEG，

∵∠AGE＝∠DGC，

∴△AGE∽△DGC，

∴＝，

∵∠AGD＝∠EGC，

∴△AGD∽△EGC，

∴∠ADG＝∠ECG，

∵Rt△ADE中，∠ADG+∠AEG＝90°，

∴∠ECG+∠ACD＝90°，即∠DCE＝90°，

∵F是DE的中点，

∴CF＝DE，

∵△ABC∽△ADE，

∴当AD⊥BC时，AD最短，此时DE最短，

当AD⊥BC时，△ABC的面积＝ADBC＝ABAC，

∴AD＝＝＝，

∵＝，即＝，

解得：DE＝4，

∴CF＝×4＝2，

故答案为：2．