题目内容
16.已知三角形AOC的顶点坐标分别为O(0,0),A($\sqrt{3}$,0),C(0,1).将△AOC沿AC翻折得到△APC.(1)P点坐标为($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$);
(2)将△PCA绕CA的中点M顺时针旋转90°到△P1C1A1的位置,点P1的坐标为(1+$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);
(3)画出相关图形.
分析 (1)在直角△OAC中,根据三角函数就可以求出∠CAO的度数,以及∠OCA的度数.而∠PCA=∠OCA,∠BCA=∠CAO,则∠PCB就可以求出.在直角△PAG中,根据三角函数可以求得AG,PG的长,从而得到P的坐标;
(2)如图2,连接MP1,由旋转的性质得到△PCA≌△△P1C1A1,△MP1C1是等边三角形,AP⊥A1P1,证得MP1∥x轴,根据M是AC的中点,即可求得结论;
(3)图2即为所做的图形.
解答 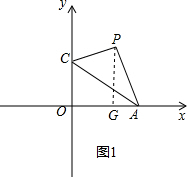 解:(1)如图1,过点P作PG⊥x轴于G,
解:(1)如图1,过点P作PG⊥x轴于G,
∵tan∠CAO=$\frac{OC}{OA}$=$\frac{\sqrt{3}}{3}$,
∴∠CAO=30°,
∴∠PAO=60°,
∵△AOC沿AC翻折得到△APC,
∴AP=$\sqrt{3}$,
∴AG=$\frac{\sqrt{3}}{2}$,PG=$\frac{3}{2}$,
∴点P的坐标为($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$);
故答案为:($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$);
(2)如图2,连接MP1,
∵将△PCA绕CA的中点M顺时针旋转90°到△P1C1A1,
∴△PCA≌△△P1C1A1,△MP1C1是等边三角形,AP⊥A1P1,
∴MP1=1,∠MP1A1=30°,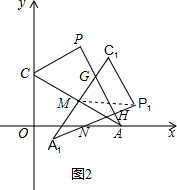
∵∠HAA1=60°,
∴∠HNA=30°,
∴∠HNA=∠MP1H,
∴MP1∥x轴,
∵M是AC的中点,
∴M($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
∴P1(1+$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
故答案为:(1+$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$).
(3)如图2所示.
点评 本题考查了折叠的性质,旋转的性质,平行线的判定好性质,坐标与图形的性质,熟练掌握各性质定理是解题的关键.

 ÷14=-156.
÷14=-156.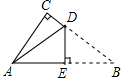 如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,求BD的长度.
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,求BD的长度.